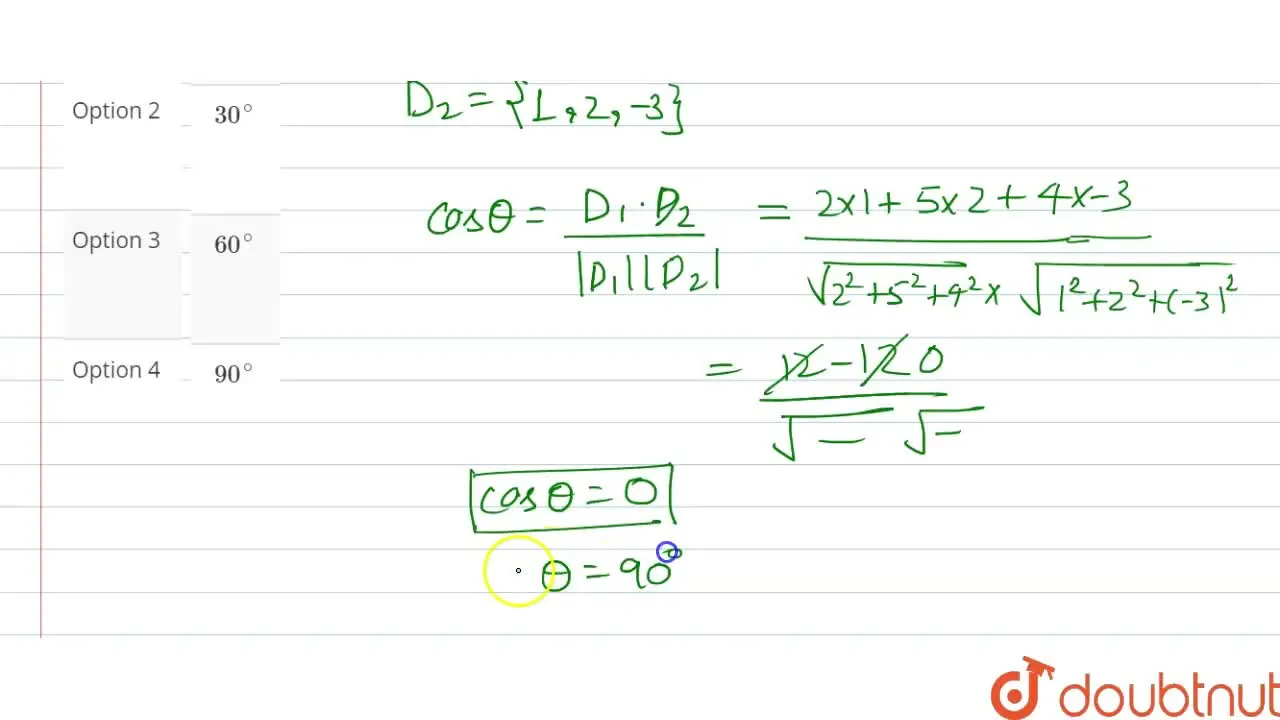The angle between the straight lines
x+12=y−25=z+34
and x−11=y+22=z−3−3 is
45∘
30∘
60∘
90∘
The correct Answer is:D
Step by step video, text & image solution for The angle between the straight lines (x+1)/(2)=(y-2)/(5)=(z+3)/(4) and (x-1)/(1)=(y+2)/(2)=(z-3)/(-3) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
The angle between the straight lines x+12=y−25=z+34andx−11=y+22=z−3−3 is 450 b. 300 c. 600 d. 900
View SolutionEquation of the angle bisector of the angle between the lines x−11=y−21=z−31andx−11=y−21=z−31 is
View SolutionEquation of the plane containing the straight line x2=y3=z4 and perpendicular to the plane containing the straight lines x2=y4=z2 and x4=y2=z3 is
View SolutionThe angle between the lines x−22=y−17=z+3−3 and x+2−1=y−42=z−54 is
View SolutionThe lines x1=y2=z3andx−1−2=y−2−4=z−3−6 are
View SolutionFind the angle between the pair of lines x+33=y−15=z+34and x+11=y−41=z−52.
View SolutionMeasure of angle between the lines
x+12=y−25=z+34 and x−11=y+22=z−3−3 isView SolutionThe lines x−21=y−32=z−43andx−1−5=y−21=z−11 are
View SolutionThe angle between lines x−22=y−3−2=z−51 and x−21=y−32=z−52 is . . . .
View Solutionv49_newFlow
View Solution