The angle of elevation of the highest point P of a vertical tower at point A on the horizontal ground is 45∘. The height of tower is 'h'/ The angle of a elevation of the tower becomes 60∘ from B on moving a distance 'd' at 30∘ angle from the horizontal. Prove that: d=h(√3−1)
To solve the problem step by step, we will analyze the given information and apply trigonometric principles.
Step 1: Understanding the Setup
We have a vertical tower of height h and two points A and B on the ground. The angle of elevation from point A to the top of the tower (point P) is 45∘. The angle of elevation from point B to the top of the tower is 60∘, and point B is reached by moving a distance d at an angle of 30∘ from the horizontal.
Step 2: Finding Distance AO
From point A, we can use the tangent of the angle of elevation:
tan(45∘)=hAO
Since tan(45∘)=1, we have:
1=hAO⟹AO=h
Hint: Recall that tan(θ)=oppositeadjacent.
Step 3: Finding Distance OB
Now, we need to find the distance OB. Since O is directly below point P and A is directly below point O, we can express AB as:
AB=AO+OB=h+OB
Step 4: Using Triangle BOP
From point B, the angle of elevation to point P is 60∘:
tan(60∘)=hOB
Since tan(60∘)=√3, we have:
√3=hOB⟹OB=h√3
Hint: Remember that tan(60∘) is a standard value.
Step 5: Finding Total Distance AB
Now substituting OB into the equation for AB:
AB=h+OB=h+h√3=h(1+1√3)=h(√3+1√3)
Step 6: Finding Distance d
The distance d can be found using the sine of the angle 30∘:
sin(30∘)=hd
Since sin(30∘)=12, we have:
12=hd⟹d=2h
Step 7: Relating d and h
We also know that d can be expressed in terms of h:
d=h(√3−1)
Conclusion
Thus, we have shown that:
d=h(√3−1)
This completes the proof.
---
We have a vertical tower of height h and two points A and B on the ground. The angle of elevation from point A to the top of the tower (point P) is 45∘. The angle of elevation from point B to the top of the tower is 60∘, and point B is reached by moving a distance d at an angle of 30∘ from the horizontal.
From point A, we can use the tangent of the angle of elevation:
tan(45∘)=hAO
Since tan(45∘)=1, we have:
1=hAO⟹AO=h
Now, we need to find the distance OB. Since O is directly below point P and A is directly below point O, we can express AB as:
AB=AO+OB=h+OB
From point B, the angle of elevation to point P is 60∘:
tan(60∘)=hOB
Since tan(60∘)=√3, we have:
√3=hOB⟹OB=h√3
Now substituting OB into the equation for AB:
AB=h+OB=h+h√3=h(1+1√3)=h(√3+1√3)
The distance d can be found using the sine of the angle 30∘:
sin(30∘)=hd
Since sin(30∘)=12, we have:
12=hd⟹d=2h
We also know that d can be expressed in terms of h:
d=h(√3−1)
Thus, we have shown that:
d=h(√3−1)
Topper's Solved these Questions
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3A
12 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3B
24 Videos
- STRAIGHT LINESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise
207 Videos
Similar Questions
The angle of elevation of the top of a tower from a point on the ground is 60∘. which is 25 m away from the foot of the tower. Find the height of the tower
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 30∘. After walking 40√3 m towards the tower, the angle of elevation becomes 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 30∘. After walking 45 m towards the tower, the angle of elevation becomes 45∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a vertical tower a point on the ground is 60∘ From another point 10 m vertical above the first, its angle of elevation is 45∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point A on the ground is 30∘. On walking 20 meters toward the tower, the angle of elevation is 60∘. Find the height of the tower and its distance from A.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
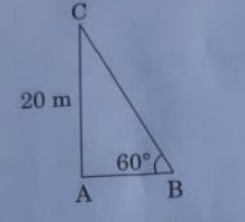
View SolutionIn figure , the angle of elevation of the top of a tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m, Find the distance of the point from the foot of the power .
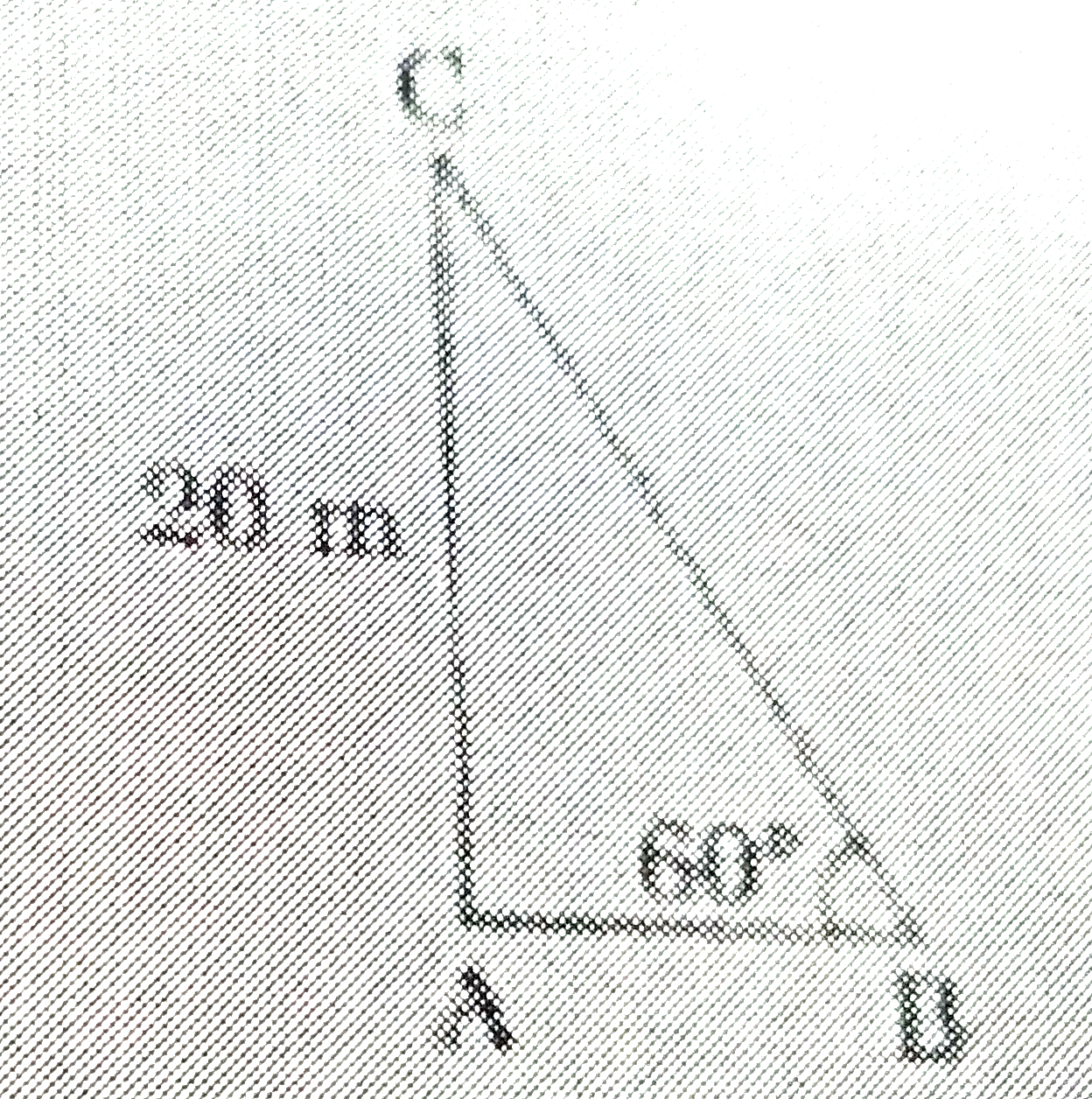
View SolutionThe angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 30°. Find the height of the tower.
View SolutionThe angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 30°. Find the height of the tower.
View Solution
