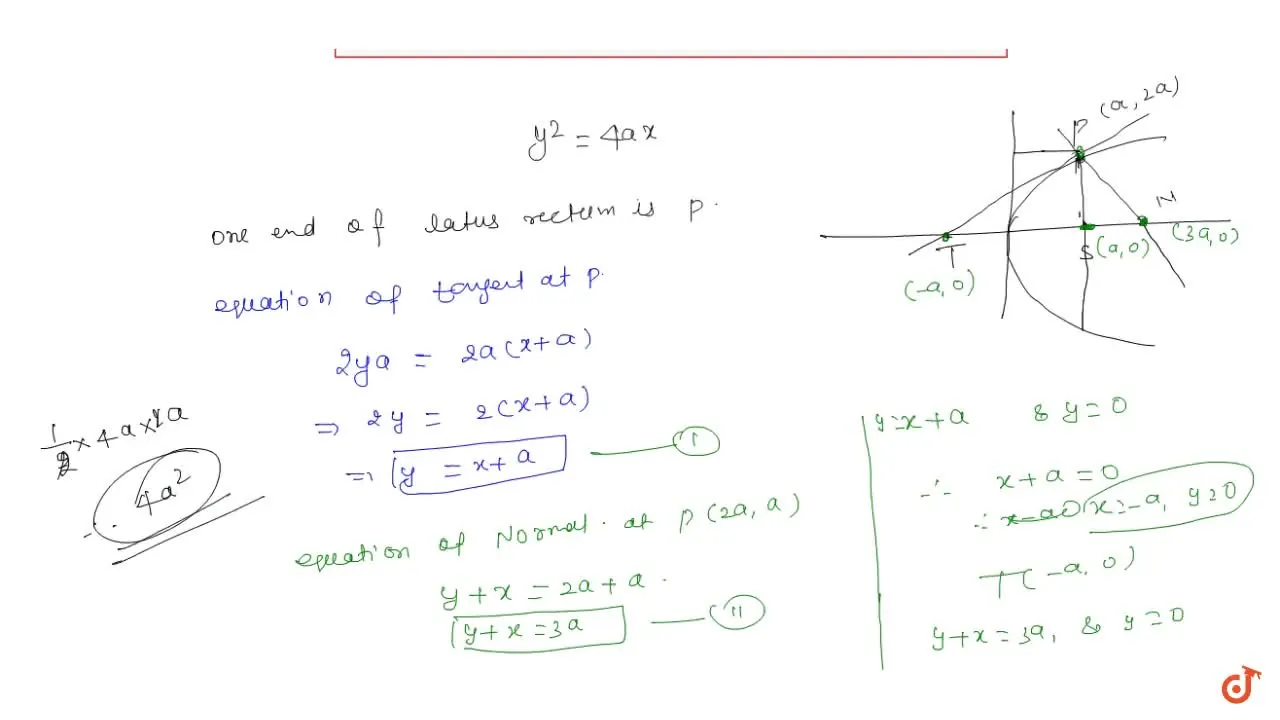
The area of the triangle formed by the tangent and the normal to the parabola y2=4ax, both drawn at the same end of the latus rectum, and the axis of the parabola is 2√2a2 (b) 2a2 4a2 (d) none of these
2√2a2
2a2
4a2
none of these
The correct Answer is:C

One end of the latus rectum is P(a,2a).
The equation of tangent PT at P(a,2a) is
2ya=2a(x+a)ory=x+a
The equation of normal PN at (a,2a) is
y+x=2a+aory+x=3a
Solving y=0 and y=x+a, we get
x=-a,y=0
Solving y=0 and y+x=3a, we get
x=3a,y=0
The area of the triangle with vertices P(a,2a),T(-a,0), and N(3a,0) is 4a2.
Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Multiple)26videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)41videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.79videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Find the equations of normal to the parabola y2=4ax at the ends of the latus rectum.
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola y2=16x to the ends of the latus rectum.
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola x2=−36y to the ends of the latus rectum.
View SolutionThe point of intersection of the normals to the parabola y2=4x at the ends of its latus rectum is
View SolutionThe triangle formed by the tangents to a parabola y2=4ax at the ends of the latus rectum and the double ordinate through the focus is
View SolutionThe normal to y2=4a(x−a) at the upper end of the latus rectum is
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus rectum
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola x2=8y to the ends of its latus rectum.
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus rectum.
View SolutionFind the area of the triangle formed by the vertex and the ends of the latus rectum of the parabola
x2=−36y.View Solution