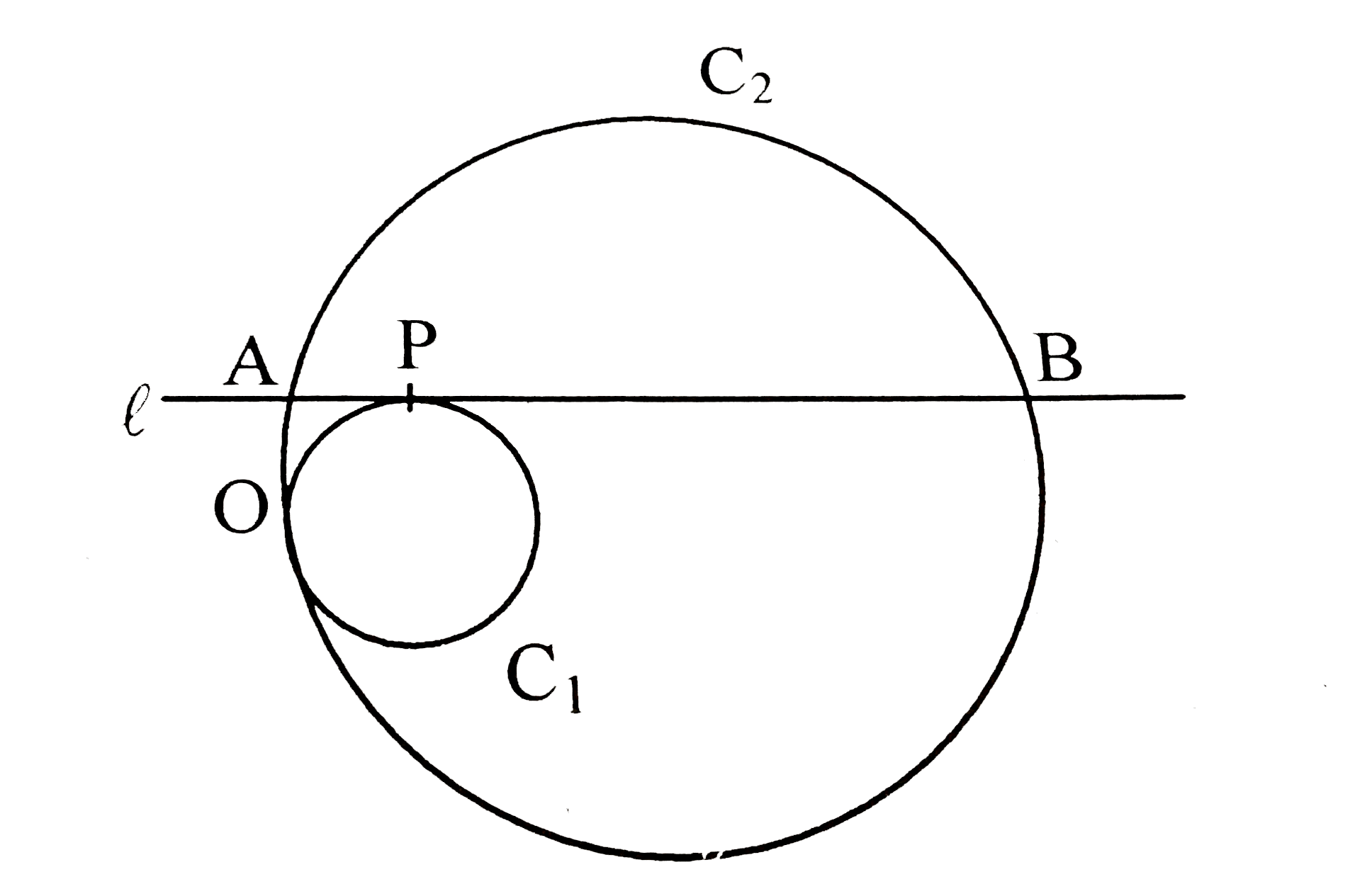
The centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
4
8
6
3
The correct Answer is:B
In δA1MP, we have
A1P2=A1M2+PM2⇒PM=√9−1=2√2
Clearly, AP is perpendicular to A1A2. Let the radius of circle C be r.
Using Pythagoras theorem in triangles APA1 and AMP, we have

AA21=AP2+A1P2andAP2=AM2+PM2
⇒(r+1)2=AP2=32andAP2=r2+(2√2)2
⇒(r+1)2=r2+8+9⇒r=8
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type12videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test31videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
Similar Questions
The centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2 and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C is
View SolutionLet C1andC2 be externally tangent circles with radius 2 and 3 respectively. Let C1andC2 both touch circle C3 internally at point A and B respectively. The tangents to C3 at A and B meet at T and TA = 4, then radius of circle C3 is :
View Solution
Knowledge Check
- Question 1 - Select One
The centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
A8B6C6√2D4√2 - Question 2 - Select One
Circles C1 and C2 of radii r and R respectively, touch each other as shown in the figure. The lime l, which is parallel to the line joining the centres of C2 and C2 is tangent to C1 at P and intersects C2 at A,B.If R2=2r2, then ∠AOB equals-
 A2212∘B45∘C60∘D6712∘
A2212∘B45∘C60∘D6712∘ - Question 3 - Select One
Let C be the circle with centre (1,1) and radius 1 . If T is the circle centred at (0,y) , passing through origin and touching the circle C externally , then the radius of T is equal to
A12B14C√3√2D√32
C1 and C2 are circle of unit radius with centers at (0, 0) and (1, 0), respectively, C3 is a circle of unit radius. It passes through the centers of the circles C1andC2 and has its center above the x-axis. Find the equation of the common tangent to C1andC3 which does not pass through C2.
View Solutionlf a circle C passing through (4,0) touches the circle x2+y2+4x−6y−12=0 externally at a point (1,−1), then the radius of the circle C is :-
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View SolutionAB is the common tangent to the circles C1 and C2. C1 and C2 are touching externally at C.AD and DC are two chords of the circle C1 and BE and CE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC
View SolutionThe line L1≡3x−4y+1=0 touches the circles C1andC2. Centers of C1 and C2 are A1(1,2) and A2(3,1) respectively Then, the length (in units) of the transverse common tangent of C1andC2 is equal to
View Solution

