The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 15), (15, 15), (0 20). Let Z = px + qy, where p,q>0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is Solution in Punjabi
p=q
p=2q
q=2p
q=3p
The correct Answer is:D
Step by step video, text & image solution for The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 15), (15, 15), (0 20). Let Z = px + qy, where p, q gt 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-II : FILL IN THE BLANKS QUESTIONS)11videos
LINEAR PROGRAMMING
- BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)10videos
LINEAR PROGRAMMING
- BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 6 MARKS7videos
LINEAR PROGRAMMING
- BOOK - ACCURATE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS CARRYING 4 MARKS27videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - ACCURATE PUBLICATIONCHAPTER - MATRICESEXERCISE - QUESTIONS CARRYING 6 MARKS4videos
MATRICES
Similar Questions
In a LPP, the linear inequalities or restrictions on the variables are called ..............
01:01View SolutionIf the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
03:04View SolutionFind the maximum value of f = x+2 y subject to the constraints
2x+3y≤6
x+4y≤4
x,y≥003:41View SolutionWrite the value of tan−1[2sin(2cos−1√32)].
03:10View SolutionIf A=⎡⎢⎣1−202130−21⎤⎥⎦,B=⎡⎢⎣72−6−21−3−425⎤⎥⎦ , find AB Also solve x−2y=10,2x+y+3z=8,−2y+z=7
03:35View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
02:13View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3),(1,1)and(3,0). Let z=px+qy, where p,q>0. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is
02:05View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
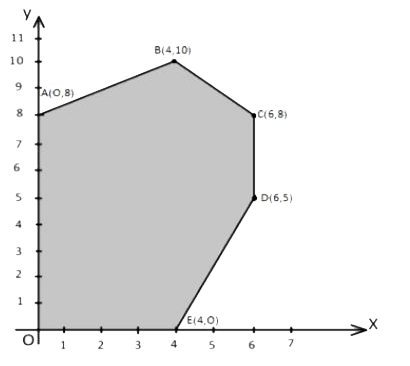
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.02:51View SolutionThe vertices of the feasible region determined by some linear constraints are (0,2),(1,1),(3,3),(1,5). Let Z=px+qy where p,q>0. The condition on pandq so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is .......
01:35View Solutionरैखिक व्यवरोधों के एक निकाय द्वारा निर्धारित, किसी सुसंगत क्षेत्र के कोनीय बिंदु (0, 10), (5, 5), (15, 15), (0, 20) हैं। मान लीजिए कि Z = px + qy, जहाँ p,q≥0. p तथा q पर लगने वाला वह प्रतिबंध, जिससे Z का अधिकतम मान (15, 15) तथा (0, 20) दोनों ही बिंदुओं पर प्राप्त हो, तब
01:50View SolutionCorner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q, so that the maximum of Z occurs at (3, 0) and (1, 1) is ……….
02:58View SolutionThe corner points of the feasible region determined by some inequality are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p,q>0 condition on p and q so that the maximum of Z occurs at both (15, 15) and (0, 20) is …………
02:28View Solutionz = 30x - 30y + 1800 is a objective function. The corner points of the feasible region are (15, 0), (15, 15), (10, 20), (0, 20) and (0, 15). z has the minimum value at …….. point.
02:33View SolutionThe vertices of the feasible region determined by some linear constraints are (0, 2), (1, 1), (3, 3), (1, 5). Let Z = px + qy where p, q gt 0. The condition on p and q so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ……..
01:28View SolutionThe correct points of the feasible region determined by the following system of linear inequalities, 2x+y≤10,x+3y≤15,x,y≥0, are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p,q>0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is ..........
01:28View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
01:28View Solution

