Question

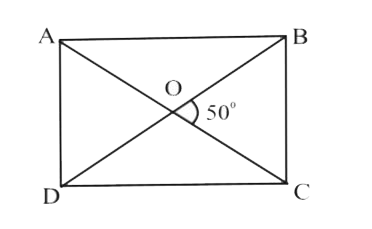
The diagonals of a rectangle PQRS intersect at O. if $\angle ROQ={60}^{\circ }$ then find $\angle OSP$.

Explanation

To solve the problem step by step, we will follow the reasoning laid out in the video transcript.

1. Understand the Given Information:
We have a rectangle PQRS with diagonals PR and QS intersecting at point O. We are given that ∠ROQ = 60°.

2. Identify Vertically Opposite Angles:
Since diagonals of a rectangle bisect each other, we know that ∠QOR is equal to ∠POS because they are vertically opposite angles.
\( \text{Thus, } \angle QOR = \angle POS = 60°. \)

3. Recognize the Properties of the Rectangle:
In a rectangle, the diagonals are equal and bisect each other. Therefore, segments OS and OP are equal:
\( OS = OP. \)

4. Set Up the Angles in Triangle OSP:
In triangle OSP, we can denote the angles as follows:
- Let ∠OSP = x
- Let ∠SPO = x (since OS = OP, the angles opposite to equal sides are equal)
- We already know ∠SOP = 60°.

5. Apply the Angle Sum Property of Triangle:
According to the angle sum property of triangles, the sum of angles in triangle OSP is 180°:
\( \angle OSP + \angle SPO + \angle SOP = 180°. \)
Substituting the known values:
\( x + x + 60° = 180°. \)

6. Solve for x:
Simplifying the equation:
\( 2x + 60° = 180°. \)
Subtract 60° from both sides:
\( 2x = 120°. \)
Now, divide by 2:
\( x = 60°. \)

7. Conclusion:
Since x represents ∠OSP, we find that:
\( \angle OSP = 60°. \)

Final Answer:
\( \angle OSP = 60°. \)