The function f is defined by f(x)={x+3 if x<1x2 if x≥1. Find f(−5),f(1),andf(3).
To solve the problem, we need to evaluate the function f(x) for the specified values of x. The function is defined as follows:
f(x)={x+3if x<1x2if x≥1
Now, we will find f(−5), f(1), and f(3) step by step.
Step 1: Finding f(−5)
1. Check the condition for x=−5:
- Since −5<1, we use the first case of the function.
2. Substitute −5 into the function:
f(−5)=−5+3
3. Calculate:
f(−5)=−2
Step 2: Finding f(1)
1. Check the condition for x=1:
- Since 1≥1, we use the second case of the function.
2. Substitute 1 into the function:
f(1)=12
3. Calculate:
f(1)=1
Step 3: Finding f(3)
1. Check the condition for x=3:
- Since 3≥1, we again use the second case of the function.
2. Substitute 3 into the function:
f(3)=32
3. Calculate:
f(3)=9
Summary of Results
- f(−5)=−2
- f(1)=1
- f(3)=9
- Since −5<1, we use the first case of the function.
2. Substitute −5 into the function:
f(−5)=−5+3
f(−5)=−2
- Since 1≥1, we use the second case of the function.
2. Substitute 1 into the function:
f(1)=12
f(1)=1
- Since 3≥1, we again use the second case of the function.
2. Substitute 3 into the function:
f(3)=32
f(3)=9
- f(1)=1
- f(3)=9
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
View Solution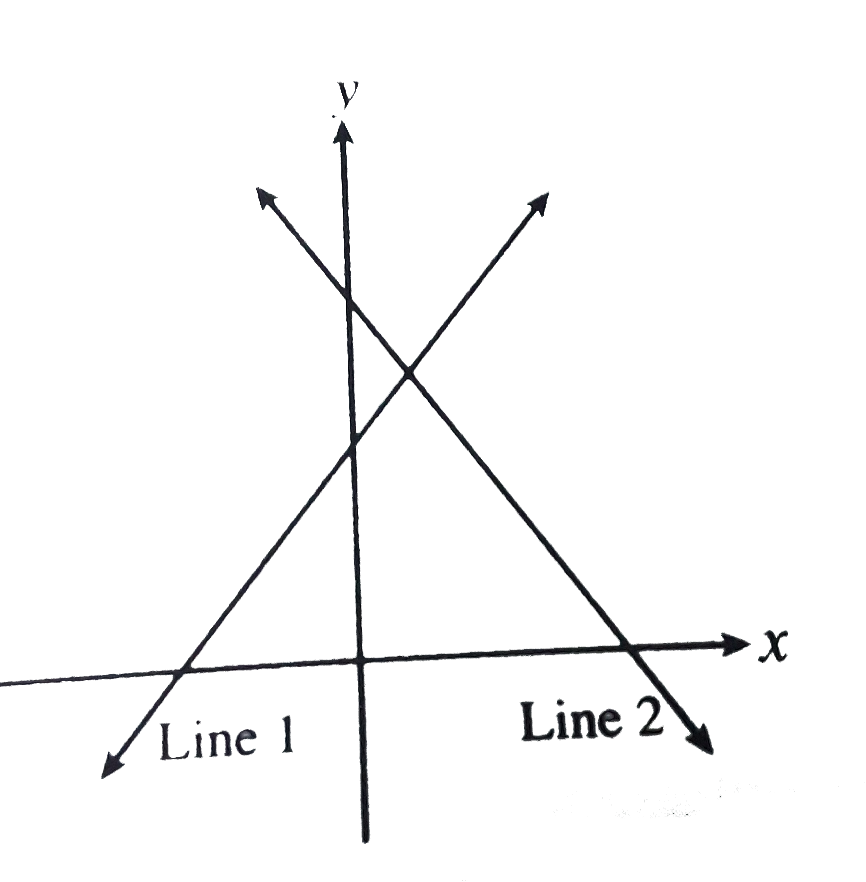
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?
View SolutionA function f is defined by f(x)=x2+1. Find f(0),f(5),f(x).
View SolutionA function f(x) is defined as f(x)=x^2+3 . Find f(0), F(1), f(x^2), f(x+1) and f(f(1)) .
View Solutionक्या f(x)={x+1, if x≥1x2+1, if x<1 द्वारा परिभाषित फलन, एक संतत फलन है?
View SolutionIf f is given by f(x)={k2x−kif x≥12if x<1 is a continuous function on R, then find k .
View SolutionA function f is defined by f(x)=3−2x. Find x such that f(x2)=(f(x))2.
View SolutionGiven that f(x)={(√x−1,x≥1),(4,x<1)}
find f(0)
View SolutionGiven that f(x)={(√x−1,x≥1),(4,x<1)}
find f(3)
View SolutionGiven that f(x)={(√x−1,x≥1),(4,x<1)}
find f(a+1) in terms of a. (Given that a≥0).
View SolutionA function f is defined by f(x)=3−2x. Find x such that f(x2)=(f(x))2.
View SolutionA function f is defined by f(x) =2x- 5 find f( -3 )
View SolutionDefine f(x)={x2+bx+c,x<1x,x≥1}.If f(x) is differentiable at x=1, then (b−c)=
View Solutionमाना f(x)[sinπx2,0≤x≤13−2x,x≥1 तब
View Solution
