The general solution of the equation sin100x−cos100x=1 is 2nπ+π3,n∈I (b) nπ+π2,n∈I nπ+π4,n∈I (d) 2nπ=π3,n∈I
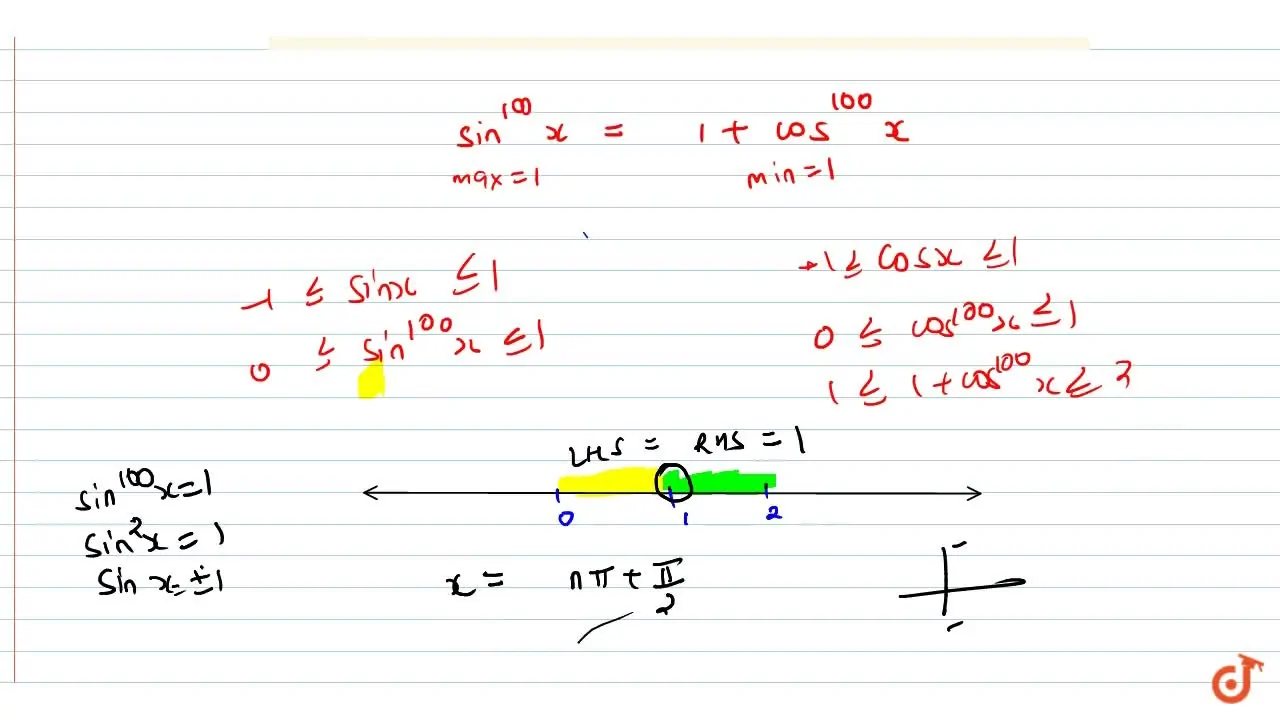
sin100x−cos100x=1
⇒sin100x=1+cos100x
Now, maximum value of sin100x can be 1.
So, above equation will satisfy only when cos100x=0.
∴sin100x=1andcos100x=0 is the only solution for this equation.
Now, sin100x=1
⇒sin2x=1
⇒sinx=±1
∴x=nπ+π2 is the general solution.
So, option (b) is the correct option.
Related Playlists
Similar Questions
The general solution of the equation sin100x−cos100x=1 is 2nπ+π3,n∈I (b) nπ+π2,n∈I nπ+π4,n∈I (d) 2nπ=π3,n∈I
View SolutionThe general solution of the equation tanx + sin(π + x) = 2sin2(x2) is/are (A) nπ,n∈I (B) 2nπ,n∈I (C) (4n+1)π4,n∈I (D) nπ+π3,n∈I
View SolutionThe general solution of the equation 2cos2x=3.2cos2x−4 is (A) x=2nπ,n∈I (B) x=nπ,n∈I (C) x=nπ4,n∈I (D) x=nπ2,n∈I
View SolutionThe solution(s) of the equation sin7x+cos2x=−2 is/are x=2kπ7+3π14, k∈I (b) x=nπ+π4 k∈I x=2nπ+π2, k∈I (d) none of these
View SolutionThe general solution of the equation 2cos2x=1=3.2−sin2x is (A) nπ,nεi (B) (n+12)π,nεI (C) (n−12)π,nεI (D) none of these
View SolutionIf solution of the equation sin42x+cos42x=sin2x.cos2x is of the form nπ2+πk,n∈I, then value of k is
View SolutionThe complete solution of the equation 7cos2x+sinxcosx−3=0 is given by (a) nπ+π2;(n∈I) (b) nπ−π4;(n∈I) (c) nπ+tan−1 43;(n∈I) (d) nπ+3π , kπ+tan−1 43;(n,k∈I)
View SolutionGeneral solution for |sinx|=cosx is (a) 2nπ+π4, n∈I (b) 2nπ±π4,n∈I (c) nπ+π4, n∈I (d) none of these
View SolutionGeneral solution of the equation s∈5θ+cos4θ=2 is (1) (4n+1)π2,n∈I (2) (4n−1)π2,n∈I (3) (2n+1)π2,n∈I (4) (6n+1)π2,n∈I
View SolutionThe roots of the equation cotx−cosx=1−cotxcosx are (1) nπ+π4,n∈I (2) 2nπ+π4,n∈I (3) 2nπ±π or nπ+π4,n∈I (4) 2nπ+π or (4n+1)π4,n∈I nπ,n∈I
View Solution