the hypotenuse of a right angle triangle is 1m less than twice the shortest side. If the third side is 1m more than the shortest side, find the sides of the triangle.
To solve the problem step by step, we will define the sides of the triangle based on the information given in the question.
Step 1: Define the sides of the triangle
Let the shortest side (base) be denoted as b.
Step 2: Express the hypotenuse in terms of the shortest side
According to the problem, the hypotenuse H is 1 meter less than twice the shortest side:
H=2b−1(Equation 1)
Step 3: Express the third side in terms of the shortest side
The third side (perpendicular) is 1 meter more than the shortest side:
P=b+1(Equation 2)
Step 4: Apply the Pythagorean theorem
According to the Pythagorean theorem, we have:
H2=P2+b2
Substituting the expressions for H and P from Equations 1 and 2 into the Pythagorean theorem gives:
(2b−1)2=(b+1)2+b2
Step 5: Expand both sides
Expanding the left side:
(2b−1)2=4b2−4b+1
Expanding the right side:
(b+1)2+b2=(b2+2b+1)+b2=2b2+2b+1
Step 6: Set the equation
Now we set the expanded forms equal to each other:
4b2−4b+1=2b2+2b+1
Step 7: Simplify the equation
Subtract 2b2+2b+1 from both sides:
4b2−4b+1−2b2−2b−1=0
This simplifies to:
2b2−6b=0
Step 8: Factor the equation
Factoring out 2b:
2b(b−3)=0
Step 9: Solve for b
Setting each factor to zero gives:
1. 2b=0 → b=0 (not valid since side lengths cannot be zero)
2. b−3=0 → b=3
Step 10: Find the other sides
Now that we have b=3:
- The perpendicular side P is:
P=b+1=3+1=4
- The hypotenuse H is:
H=2b−1=2(3)−1=6−1=5
Final Answer
The sides of the triangle are:
- Shortest side (base) = 3 m
- Perpendicular side = 4 m
- Hypotenuse = 5 m
---
Let the shortest side (base) be denoted as b.
According to the problem, the hypotenuse H is 1 meter less than twice the shortest side:
H=2b−1(Equation 1)
The third side (perpendicular) is 1 meter more than the shortest side:
P=b+1(Equation 2)
According to the Pythagorean theorem, we have:
H2=P2+b2
Substituting the expressions for H and P from Equations 1 and 2 into the Pythagorean theorem gives:
(2b−1)2=(b+1)2+b2
Expanding the left side:
(2b−1)2=4b2−4b+1
Expanding the right side:
(b+1)2+b2=(b2+2b+1)+b2=2b2+2b+1
Now we set the expanded forms equal to each other:
4b2−4b+1=2b2+2b+1
Subtract 2b2+2b+1 from both sides:
4b2−4b+1−2b2−2b−1=0
This simplifies to:
2b2−6b=0
Factoring out 2b:
2b(b−3)=0
Setting each factor to zero gives:
1. 2b=0 → b=0 (not valid since side lengths cannot be zero)
2. b−3=0 → b=3
Now that we have b=3:
- The perpendicular side P is:
P=b+1=3+1=4
- The hypotenuse H is:
H=2b−1=2(3)−1=6−1=5
The sides of the triangle are:
- Shortest side (base) = 3 m
- Perpendicular side = 4 m
- Hypotenuse = 5 m
Topper's Solved these Questions
Similar Questions
The hypotenuse of a right triangle is 6 m more than the twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle.
View SolutionThe diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
View SolutionThe diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
View SolutionThe diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
View SolutionThe longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm, then find the minimum length of the shortest side.
View SolutionThe longest side of a triangle is twice the shortest side and the third side is 3 cm longer than the shortest side. If the perimeter of the triangle is at least 39 cm, find the minimum length of the longest side.
View SolutionThe longest side of a triangle is three times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
View SolutionThe longest side of a triangle is three times the shortest side and the third side is 2 cm shorter than the longest side if the perimeter of the triangles at least 61 cm, find the minimum length of the shortest side.
View SolutionFind the length of the third side of the triangle.
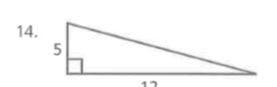
View SolutionFind the length of the third side of the triangle.
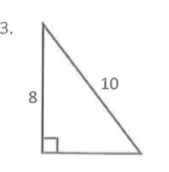
View Solution
