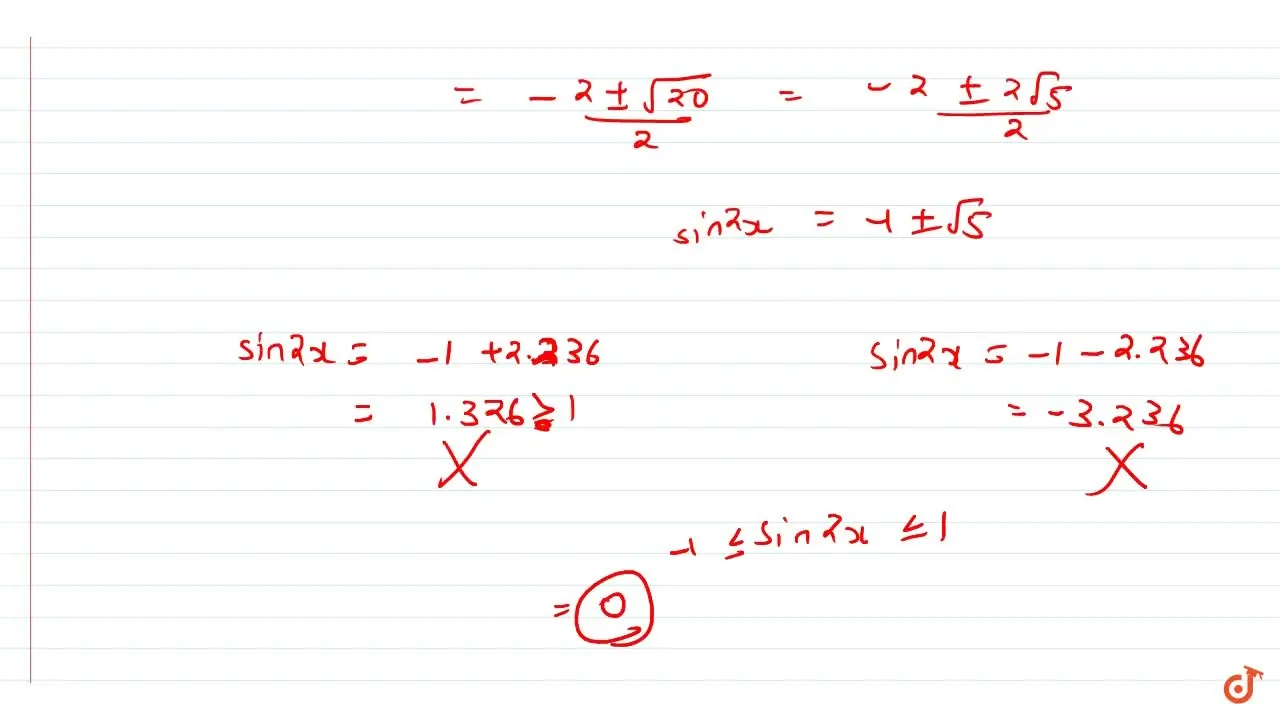The number of solutions of the equation sin3xcosx+sin2xcos2x+sinxcos3x=1 in the interval [0,2π] is/are 0 (b) 2 (c) 3 (d) infinite
sin3xcosx+sin2xcos2x+sinxcos3x=1
sinxcosx(sin2x+sinxcosx+cos2x)=1
sinxcosx(1+sinxcosx)=1
sin2x2⋅[1+sin2x2]=1
sin22x+2sinx−4=0
sin2x=−2±√4+162
=−2±√202=−1±√5
sin2x=−1+2.326=1.326≥1
sin2x=−1−2.236=−3.236
−1≤sin2x≤1
=0
Option A is correct.
Related Playlists
Similar Questions
The number of solutions of the equation sin3xcosx+sin2xcos2x+cos3xsinx=1 in the interval [0,2π] is /are
View SolutionThe number of solutions of the equation sin3xcosx+sin2xcos2x+sinxcos3x=1 in the interval [0,2π] is/are 0 (b) 2 (c) 3 (d) infinite
View SolutionSolve the equation sin3xcosx−sinxcos3x=14
View SolutionThe number of solutions of the equation 2(sin3x+cos3x)−3(sinx+cosx)+8=0 in the interval (0,4π) is
View SolutionThe number of solutions of the equation 2(sin3x+cos3x)−3(sinx+cosx)+8=0 in the interval (0,4π) is
View SolutionThe number of solutions of the equation 2(sin3x+cos3x)−3(sinx+cosx)+8=0 in the interval (0,4π) is
View SolutionThe number of solutions of the equation 2(sin3x+cos3x)−3(sinx+cosx)+8=0 in the interval (0,4π) is
View SolutionThe number of solution of the equation sin3xcosx+sin2xcos2x+cos3xsinx+1=0 in the interval [0,2π] is equal to
View SolutionThe number of solutions of the equation 2(sin42x+cos42x)+3sin2xcos2x=0 is
View SolutionNumber of solutions of the equation
sin5x⋅cos3x=sin6x⋅cos2x,
In the interval [0,π] isView Solution