The number of solutions of the equation [y+[y]]=2cosx, where y=13[sinx+[sinx+[sinx]]] (where [.] denotes the greatest integer function) is
A
4
B
2
C
3
D
0
Video Solution
Text Solution
The correct Answer is:D
[y+[y]]=2cosx
or[y]+[y]=2cosx (∵[x+n]=[x]+n if n∈I)
or2[y]=2cosxor[y]=cosx (1)
Also, y=13[sinx+[sinx+[sinx]]]
=13(3[sinx])
=[sinx] (2)
From (1) and (2),
[[sinx]]=cosx
or[sinx]=cosx
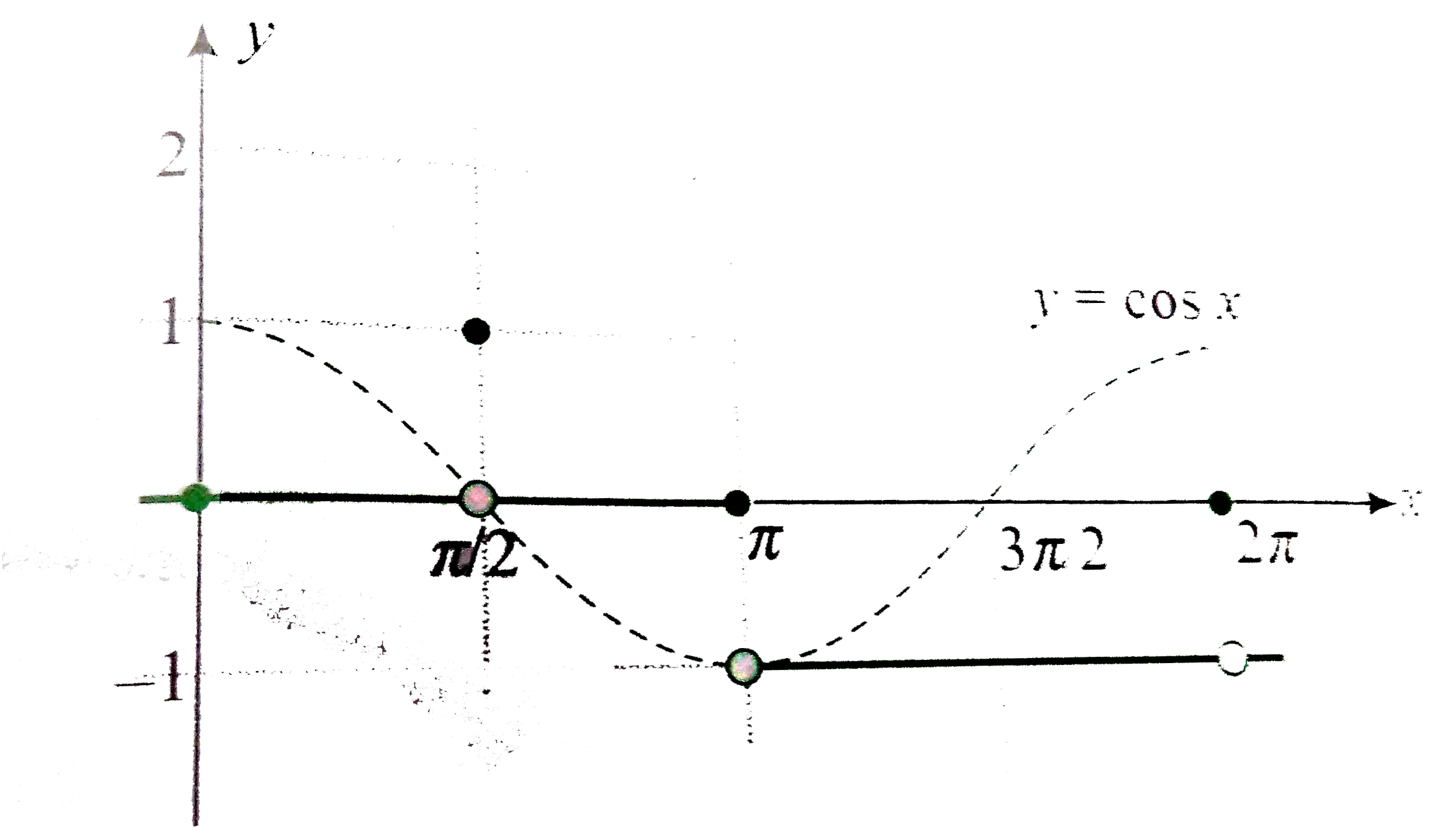
The number of solutions is 0.
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.15
8 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Knowledge Check
f(x)=[sinx] where [.] denotest the greatest integer function is continuous at:
Ax=π2Bx=πCx=3π2Dx=2πNumber of solutions of the equations y=13[sinx+[sinx+[sinx]]]and[y+[y]]=2cosx, where [.] denotes the greatest integer function is:
A0B1C2DinfiniteDomain of the function f(x)=1[sinx−1] (where [.] denotes the greatest integer function) is
AR~{2nπ+π2,n∈l}BR~{nπ+π2,n∈l)}C[2nπ,2nπ+π2]Dnone of these
Draw the graph of y=[|x|], where [.] denotes the greatest integer function.
View Solutionlimx→0e[|sinx|][x+1] is , where [.] denotes the greatest integer function.
View SolutionThe range of the function f(x)=[sinx+cosx] (where [x] denotes the greatest integer function) is f(x)∈ :
View SolutionIf I=∫20π−20π|sinx|[sinx]dx (where [.] denotes the greatest integer function) then the value of I is
View SolutionThe number of solutions of the equations y=13[sinθ+[sinθ+[sinθ]]]and[y+[y]]=2cosθ [ where , [.] denote the greatest integer function ] is/are
View Solution
