The perimeter of a circle and its diameter vary _______ with each other.
To solve the question about how the perimeter of a circle and its diameter vary with each other, we can follow these steps:
1. Understand the Terms:
- The perimeter of a circle is also known as the circumference.
- The diameter is the distance across the circle through its center.
2. Formula for Circumference:
- The formula for the circumference (C) of a circle is given by:
C=π×d
where d is the diameter of the circle and π (pi) is a constant approximately equal to 3.14 or 227.
3. Relationship Between Circumference and Diameter:
- From the formula, we can see that the circumference is directly proportional to the diameter. This means that if the diameter increases, the circumference also increases, and vice versa.
4. Proportionality Statement:
- We can express this relationship mathematically as:
C∝d
- This indicates that the circumference (C) varies directly with the diameter (d).
5. Conclusion:
- Therefore, we conclude that the perimeter of a circle and its diameter vary directly proportional to each other.
Final Answer:
The perimeter of a circle and its diameter vary directly proportional with each other.
---
- The perimeter of a circle is also known as the circumference.
- The diameter is the distance across the circle through its center.
- The formula for the circumference (C) of a circle is given by:
C=π×d
where d is the diameter of the circle and π (pi) is a constant approximately equal to 3.14 or 227.
- From the formula, we can see that the circumference is directly proportional to the diameter. This means that if the diameter increases, the circumference also increases, and vice versa.
- We can express this relationship mathematically as:
C∝d
- This indicates that the circumference (C) varies directly with the diameter (d).
- Therefore, we conclude that the perimeter of a circle and its diameter vary directly proportional to each other.
The perimeter of a circle and its diameter vary directly proportional with each other.
Topper's Solved these Questions
- DIRECT AND INVERSE PROPORTIONS BOOK - NCERT EXEMPLARCHAPTER - DIRECT AND INVERSE PROPORTIONS EXERCISE - THINK AND DISCUSS
2 Videos
- DIRECT AND INVERSE PROPORTIONS BOOK - NCERT EXEMPLARCHAPTER - DIRECT AND INVERSE PROPORTIONS EXERCISE - THINK AND DISCUSS
2 Videos
- DATA HANDLINGBOOK - NCERT EXEMPLARCHAPTER - DATA HANDLINGEXERCISE - EXERCISE
73 Videos
- EXPONENTS AND POWERSBOOK - NCERT EXEMPLARCHAPTER - EXPONENTS AND POWERSEXERCISE - EXERCISE
195 Videos
Similar Questions
Knowledge Check
If the perimeter of a triangle and the diameter of an ex-circle are equal , then the triangle is
Aright angled isoscelesBright angledCequilateralDisoscelesIf the perimeter of a sector of a circle is twice the diameter of the circle, then the radian measure of the angle of the sector is
A2Bπ2CπD4
If xy = 10, then x and y vary ______ with each other.
View SolutionIf the diameter of a circle is d, then its perimeter is
View SolutionLength of a side of a square and its area vary directly with each other.
View SolutionIf the perimeter of a circle is numerically equal to its area, find the radius of the circle.
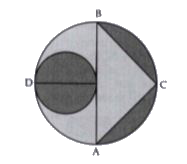
View SolutionIn figure , AB and CD are two diameters of a circle ( with centre O) perpendicular to each other and OD is the diameter of the smaller circle . If OA = 7 cm , find the area of the shaded region.
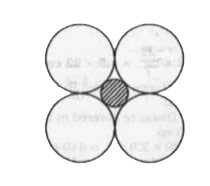
View SolutionIn the figure given below, D is the diameter of each circle. What is the diameter of the shaded circle ?
View Solution
