Question

The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at
B, Find the values of p.

Options

A. 7
B. 3
C. 5
D. 4

Answer

D

Explanation

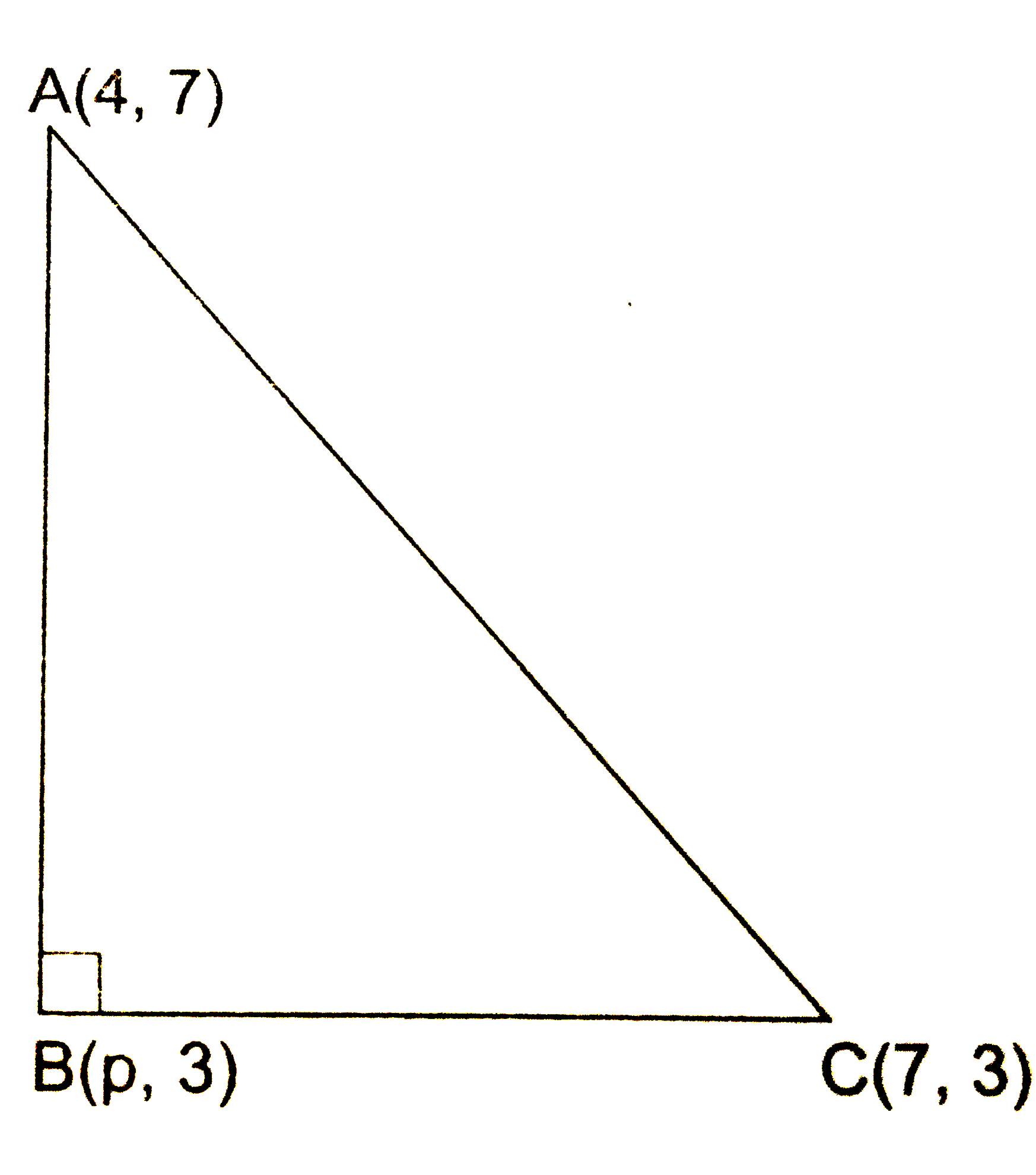
Since `Delta ABC` is a right angled at B, we have
`AB^(2) + BC^(2) = AC^(2)`
`rArr {(p-4)^(2) + (3-7)^(2)} + {(7-p)^(2)+ (3-3)^(2)} = (7-4)^(2) + (3-7)^(2)`
`rArr (p-4)^(2) + (-4)^(2) + (7-p)^(2) +0 = 3^(2) + (-4)^(2)`
`rArr 2p^(2) -22p + (16+49+16) = 9+16`
`rArr 2p^(2) -22p +56 = 0`
`rArr p^(2) -11p +28 = 0`
`rArr p^(2)-7p-4p +28 =0`
`rArr p(p-7)-4(p-7) = 0`
`rArr (p-7)(p-4) = 0`
`rArr p-7 =0 " or " p-4 = 0`
`rArr p =7 " or " p = 4`
When p = 7 then the points B and C coincide and so no triangle is formed in this case.
So, `p ne 7`. Hence, p = 4