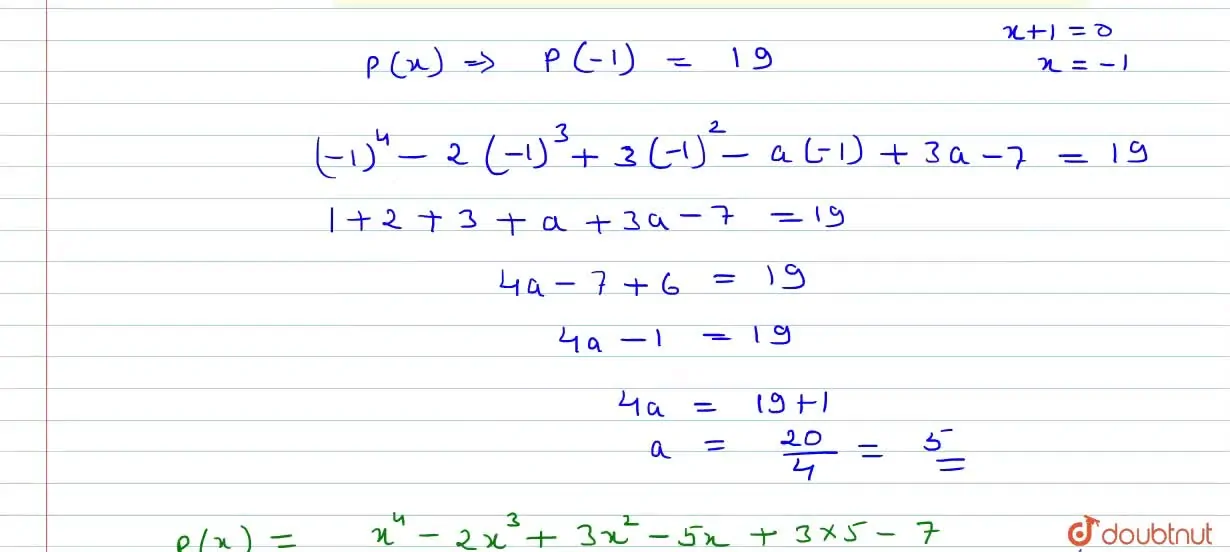the polynomial p(x)=x4−2x3+3x2−ax+3a−7 when divided by x+1 leaves the remainder 19. find the values of A , also find the remainder when p(x) is divided by x+2.
Given p(x)=x4−2x3+3x2−ax+3a−7
when we divide p(x) by x+1 ,then we get the the reamainder p(-1)
Now , P(−1)=(−1)4−2(−1)3+3(−1)3+3(−1)2−a(−1)+3a−7
=1+2+3+a+3a−7=4a−1
According to the question p(−1)=19
⇒4a−1=19
⇒4a−1=19
⇒4a=20
∴a=5
∴ Required polynomial =x4−2x3+3x2−5x+3(5)−7
=x4−2x3+3x2−5x+15−7
=x4−2x3+3x2−5x+8
when we divide p(x) by x+2 then we get the remainder p(-2),
Now , P(−2)=(−2)4−2(−2)3+3(−2)3+3(−2)2−5(−2)+8
=16+16+12+10+8=62
hence ,the value of a is 5 and remainder is 62 .
Related Playlists
Similar Questions
The polynomial p(x)=x4−2x3+3x2−ax+3a when divided by (x+1) leaves the remainder 19. Find the value of a .
View SolutionThe polynomials (2x3+x2−ax+2)and(2x3−3x2−3x+a) when divided by (x−2) leave the same remainder . Find the value of a.
View SolutionThe polynomialsf(x)=x4−2x3+3x2−ax+b when divided by (x−1)and (x+1) leaves the remainders 5 and 19 respectively. Find the values of a and b.. Hence, find the remainder when f(x) is divided by (x-2).
View SolutionIf the polynomial P(x)=x4−2x3+3x2−ax+3a−7 when divided by (x+1) leaves the remainder 19, then what is the remainder when P(x) is divided by x+2?
View SolutionThe polynomial ax3−29x2+45x−9 when divided by (3x−1) leaves remainder 3 . Find the value of a Also, find the remainder when the given polynomial is divided by x−2 .
View SolutionThe polynomial
f(x)=ax3+9x2+4x−8, when divided by (x+3) leaves the remainder (-20). Then , the value of a isView SolutionThe polynomial p(x)=x4−2x3−ax+3a−7 when divided by x+1 leaves remainder 19. Also, find the remainder when p(x) is divided by x+2.
View SolutionPolynomials ax3+3x2−3 and2x3−5x+a when divided by (x−4) leave the same remainder. Find the value of a.
View SolutionThe polynomial f (x)= x4+2x3+3x2−ax+bwhen divided by (x-1) and (x + 1) leaves the remainders 5 and 19 respectively. Find the values of a and b. Hence, find the remainder when f (x) is divided by (x-2)
View SolutionIf the polynomials ax3+3x2−13 and 2x3−5x+a, when divided by (x−2) leave the same remainder, find the value of a .
View Solution