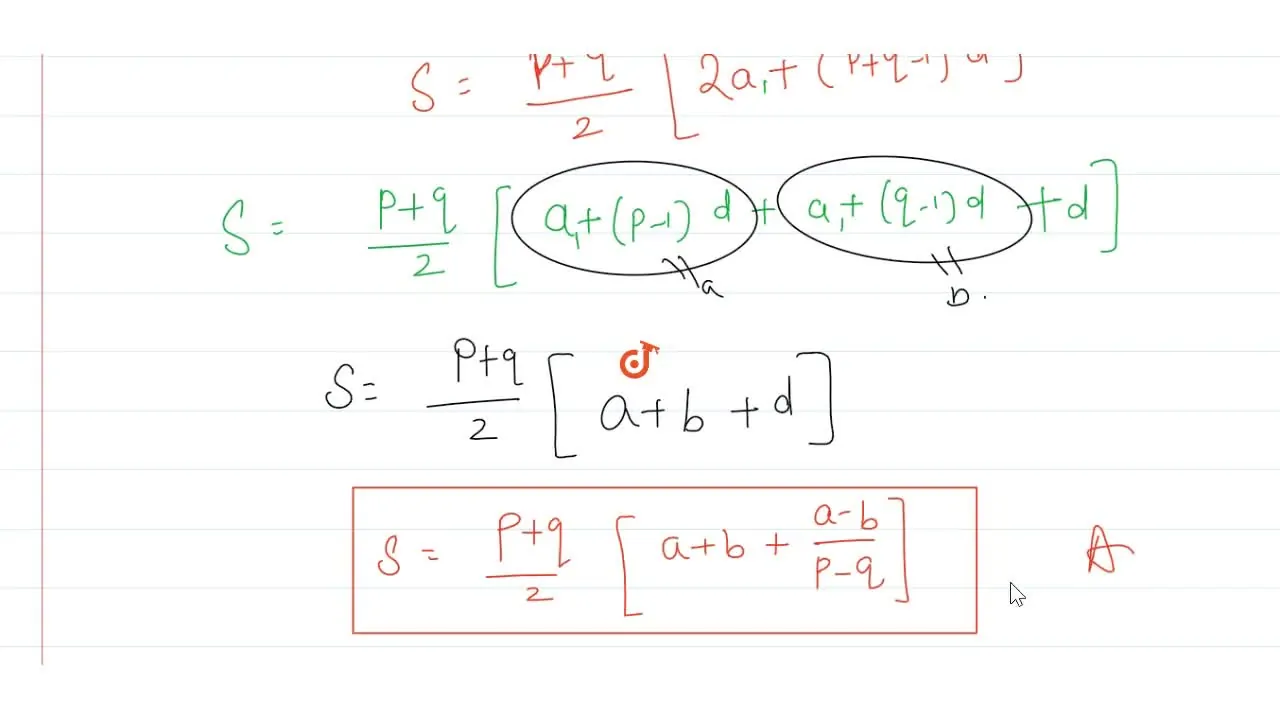
The term of an A.P. is and term is Prove that the sum of its terms is
subtracting equation 2 from 1
Sum of p+q terms
.
Related Playlists
Similar Questions
The pth term of an A.P. is a and qth term is b Prove that the sum of its (p+q) terms is p+q2{a+b+a−bp−q}.
View SolutionThe pth term of an A.P. is aandqth term is b. Prove that the sum of its (p+q) terms is p+q2{a+b+a−bp−q}.
View SolutionIf the pth term of an A.P is q and qth term is p, prove that its nth term is (p+q-n)
View SolutionIf p th term of an A.P. is 1q and q th term is 1p prove that the sum of the first pq terms is 12[pq+1]
View SolutionThe pth term of an A.P. is a and qth term is b. Then find the sum of its (p+q) terms.
View SolutionIf the pth term of an A.P. is q and the qth term is p, prove that its nthtermis(p+q−n).
View SolutionIf pth term of an A.P.is q and the qth term is p.Find the first term of the A.P.
View SolutionIf pth term of an A. P. is q and the qth term is p. Find the first term of an A.P.
View Solutionif the pth term of an A.P. is x and qth term is y, show tht the sum of (p+q) terms is p+q2[x+y+(x−yp−q)]
View SolutionThe first term of an A.P. is a and the sum of first p terms is zero, show tht the sum of its next q terms is a(p+q)qp−1.
View Solution