The sum of the three vectors determined by the medians of triangle directed from the vertices is
0
1
−1
13
The correct Answer is:A
To find the sum of the three vectors determined by the medians of a triangle directed from the vertices, we can follow these steps:
1. Identify the Triangle and Medians:
Let the vertices of the triangle be A, B, and C. The midpoints of the sides BC, CA, and AB are denoted as D, E, and F, respectively. The medians are the segments AD, BE, and CF.
2. Express the Medians as Vectors:
- The median AD can be expressed as:
→AD=→AB+→BD
Since D is the midpoint of BC, we have:
→BD=12→BC
Thus,
→AD=→AB+12→BC
- For the median BE:
→BE=→BC+→CE
Here, E is the midpoint of CA, so:
→CE=12→CA
Therefore,
→BE=→BC+12→CA
- For the median CF:
→CF=→CA+→AF
Since F is the midpoint of AB:
→AF=12→AB
Thus,
→CF=→CA+12→AB
3. Sum the Medians:
Now, we need to sum the three medians:
→AD+→BE+→CF
Substituting the expressions we derived:
→AD+→BE+→CF=(→AB+12→BC)+(→BC+12→CA)+(→CA+12→AB)
Combining like terms:
=→AB+12→AB+→BC+12→BC+→CA+12→CA
=(1+12)→AB+(1+12)→BC+(1+12)→CA
=32→AB+32→BC+32→CA
4. Factor Out Common Terms:
=32(→AB+→BC+→CA)
5. Recognize the Vector Sum:
The sum →AB+→BC+→CA represents a closed triangle path, which equals zero:
→AB+→BC+→CA=→0
6. Final Result:
Therefore, the sum of the three medians is:
32⋅→0=→0
Conclusion:
The sum of the three vectors determined by the medians of the triangle directed from the vertices is →0.
---
Let the vertices of the triangle be A, B, and C. The midpoints of the sides BC, CA, and AB are denoted as D, E, and F, respectively. The medians are the segments AD, BE, and CF.
- The median AD can be expressed as:
→AD=→AB+→BD
Since D is the midpoint of BC, we have:
→BD=12→BC
Thus,
→AD=→AB+12→BC
→BE=→BC+→CE
Here, E is the midpoint of CA, so:
→CE=12→CA
Therefore,
→BE=→BC+12→CA
→CF=→CA+→AF
Since F is the midpoint of AB:
→AF=12→AB
Thus,
→CF=→CA+12→AB
Now, we need to sum the three medians:
→AD+→BE+→CF
→AD+→BE+→CF=(→AB+12→BC)+(→BC+12→CA)+(→CA+12→AB)
=→AB+12→AB+→BC+12→BC+→CA+12→CA
=(1+12)→AB+(1+12)→BC+(1+12)→CA
=32→AB+32→BC+32→CA
=32(→AB+→BC+→CA)
The sum →AB+→BC+→CA represents a closed triangle path, which equals zero:
→AB+→BC+→CA=→0
Therefore, the sum of the three medians is:
32⋅→0=→0
The sum of the three vectors determined by the medians of the triangle directed from the vertices is →0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The point where the all three medians of a triangle meet is called
ACentroidBIncentreCCircumcentreDOrthocentre - Question 2 - Select One
What is the measure of the hypotenuse of a right triangle, when its medians, drawn from the vertices of the acute angles, are 5 cm and 2√10cm
A5√8cmB2√13cmC6√10cmD2√7cm
The sum of these three vectors is :
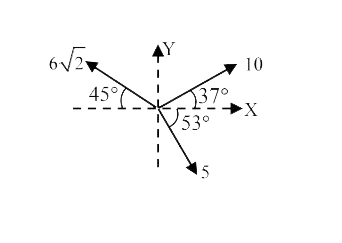 View Solution
View SolutionThree coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
View SolutionPoint where three medians of a triangle meet.
View SolutionFind the vector from the origin to the intersection of the medians of the triangle whose vertices are A(-1,-3) B(5, 7) and C(2, 5).
View SolutionFind the vector from the origin to the intersection of the medians of the triangle whose vertices are A(−1,−3),B(5,7)andC(2,5).
View SolutionWhat is the measure of the hypotenuse of a right triangle, when its medians, drawn from the vertices of the acute angles, are 5 cm and 2√10 cm long ?
View Solution

