△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
To prove that line AD bisects BC at right angles in the given isosceles triangles ABC and DBC, we will follow these steps:
1. Draw the Diagram:
- Draw triangle ABC and triangle DBC on the same base BC.
- Mark the points A, B, C, and D appropriately.
2. Identify Given Information:
- Triangle ABC is isosceles, which means AB = AC.
- Triangle DBC is also isosceles, which means DB = DC.
3. Establish Congruent Triangles:
- We will show that triangles ABD and ACD are congruent.
- From the information given:
- AB = AC (since triangle ABC is isosceles)
- BD = DC (since triangle DBC is isosceles)
- AD is common to both triangles.
4. Use the SSS Congruence Criterion:
- By the Side-Side-Side (SSS) congruence criterion, we can conclude:
- Triangle ABD ≅ Triangle ACD.
5. Conclude Angles:
- Since the triangles are congruent, the angles opposite to equal sides are also equal:
- ∠ABD = ∠ACD (by CPCT - Corresponding Parts of Congruent Triangles are Equal).
6. Show that AD Bisects BC:
- Since ∠ABD = ∠ACD, this implies that line AD bisects angle A, which means it divides BC into two equal segments.
- Let P be the point where AD intersects BC. Thus, BP = PC.
7. Prove Right Angles:
- Since triangles ABD and ACD are congruent, and AD is the angle bisector, it also implies that ∠APB = ∠APC.
- Since these angles are equal and sum to 180 degrees, each must be 90 degrees.
- Therefore, AD is perpendicular to BC.
8. Final Conclusion:
- We have shown that line AD bisects BC at right angles, completing the proof.
- Draw triangle ABC and triangle DBC on the same base BC.
- Mark the points A, B, C, and D appropriately.
- Triangle ABC is isosceles, which means AB = AC.
- Triangle DBC is also isosceles, which means DB = DC.
- We will show that triangles ABD and ACD are congruent.
- From the information given:
- AB = AC (since triangle ABC is isosceles)
- BD = DC (since triangle DBC is isosceles)
- AD is common to both triangles.
- By the Side-Side-Side (SSS) congruence criterion, we can conclude:
- Triangle ABD ≅ Triangle ACD.
- Since the triangles are congruent, the angles opposite to equal sides are also equal:
- ∠ABD = ∠ACD (by CPCT - Corresponding Parts of Congruent Triangles are Equal).
- Since ∠ABD = ∠ACD, this implies that line AD bisects angle A, which means it divides BC into two equal segments.
- Let P be the point where AD intersects BC. Thus, BP = PC.
- Since triangles ABD and ACD are congruent, and AD is the angle bisector, it also implies that ∠APB = ∠APC.
- Since these angles are equal and sum to 180 degrees, each must be 90 degrees.
- Therefore, AD is perpendicular to BC.
- We have shown that line AD bisects BC at right angles, completing the proof.
Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - MULTIPLE CHOICE QUESTIONS
15 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
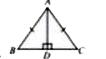
AD bisects BC
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
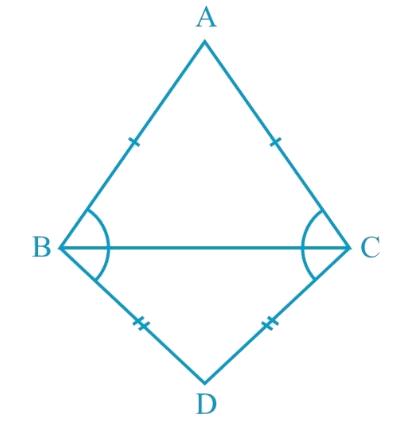
View SolutionIn Figure, ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that ∠ABD= ∠ACD
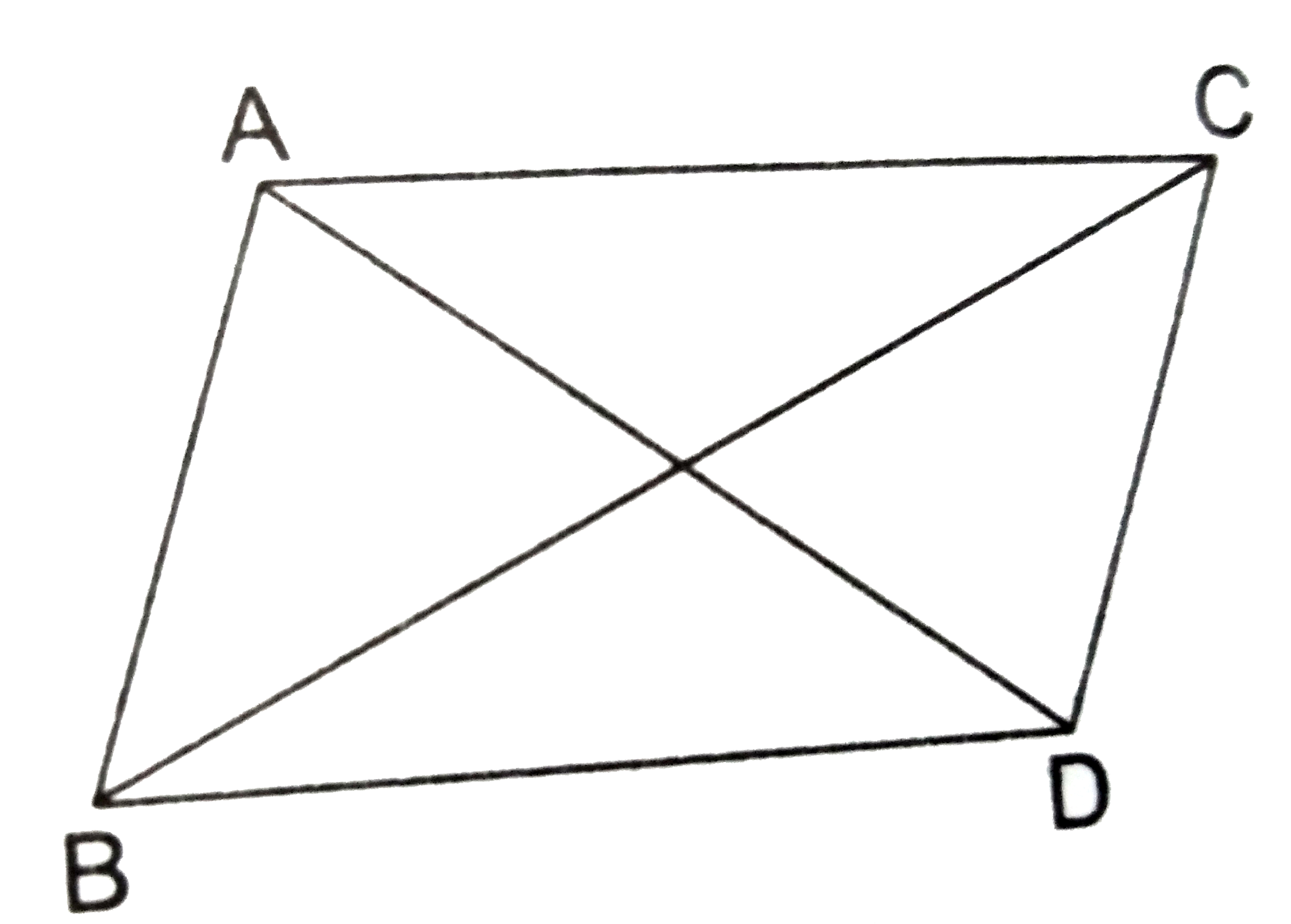
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
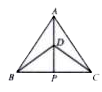
AP bisects ∠A as well as ∠D.
View SolutionIf two isosceles triangles have a common base, prove that the line joining their vertices bisects them at right angles.
View Solution
