Two circles with centres O and O' of radii 3cm and 4 cm, respectively intersect at two points P and Q, such that OP and O' P are tangents to the two circles. Find the length of the common chord PQ.Solution in Tamil
The correct Answer is:PQ = 4.8 cm
Step by step video, text & image solution for Two circles with centres O and O' of radii 3cm and 4 cm, respectively intersect at two points P and Q, such that OP and O' P are tangents to the two circles. Find the length of the common chord PQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO EXERCISE 4.5
15 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO UNIT EXERCISE
13 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO EXERCISE 4.3
8 Videos
- CO-ORDINATE GEOMETRY BOOK - PREMIERS PUBLISHERSCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Other Important Objective
25 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
Similar Questions
If in triangles ABC and EDF, ABDE=BCFD then they will be similar, when
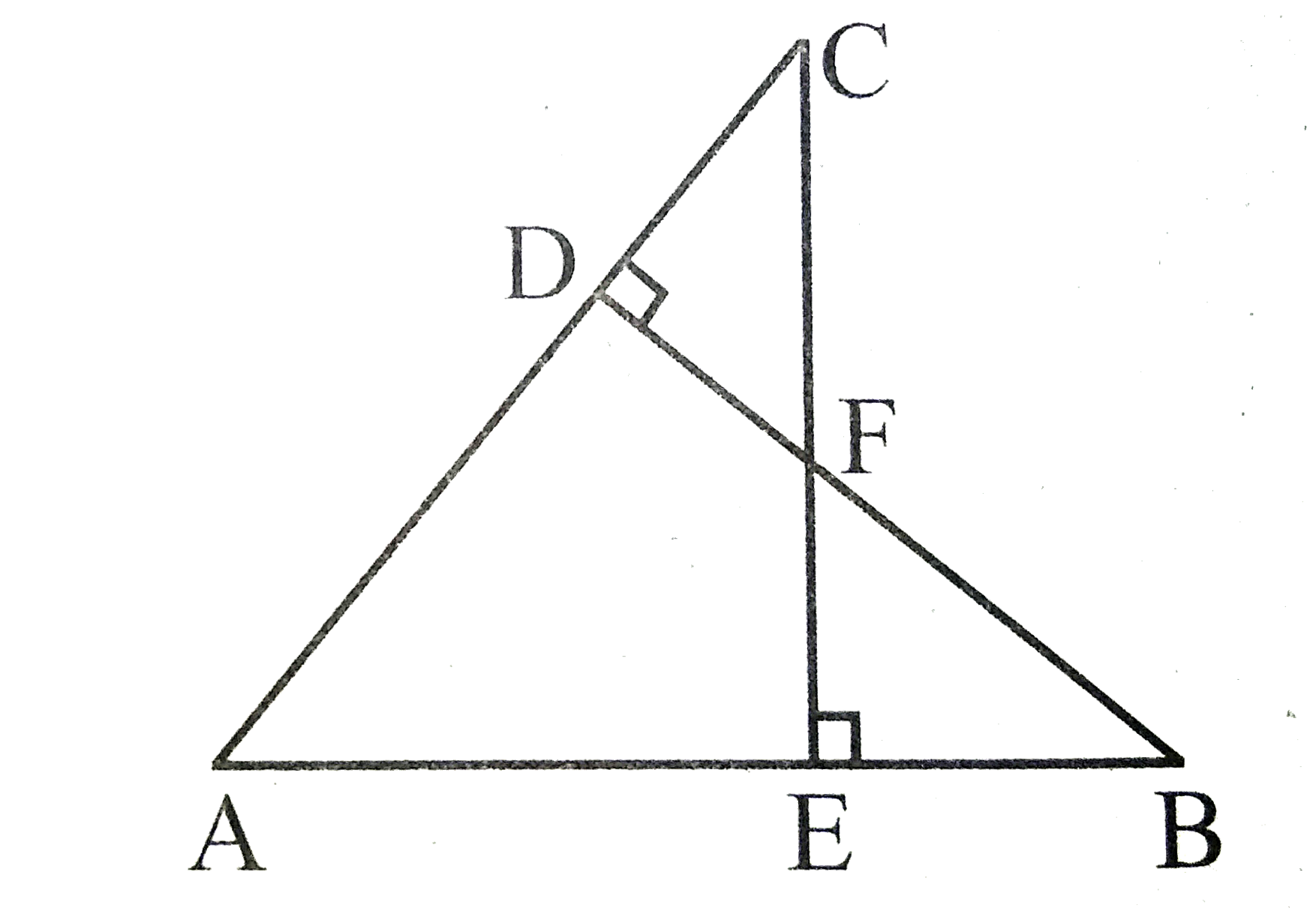
View SolutionIn the figure, if BD⊥ACandCE⊥AB , prove that
(i)ΔAEC~ΔADB (ii)CAAB=CEDB
View SolutionA man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
View SolutionThe area of the triangle formed by the points (0,0),(3,0) and (0,4) is :
View SolutionMatch the following:
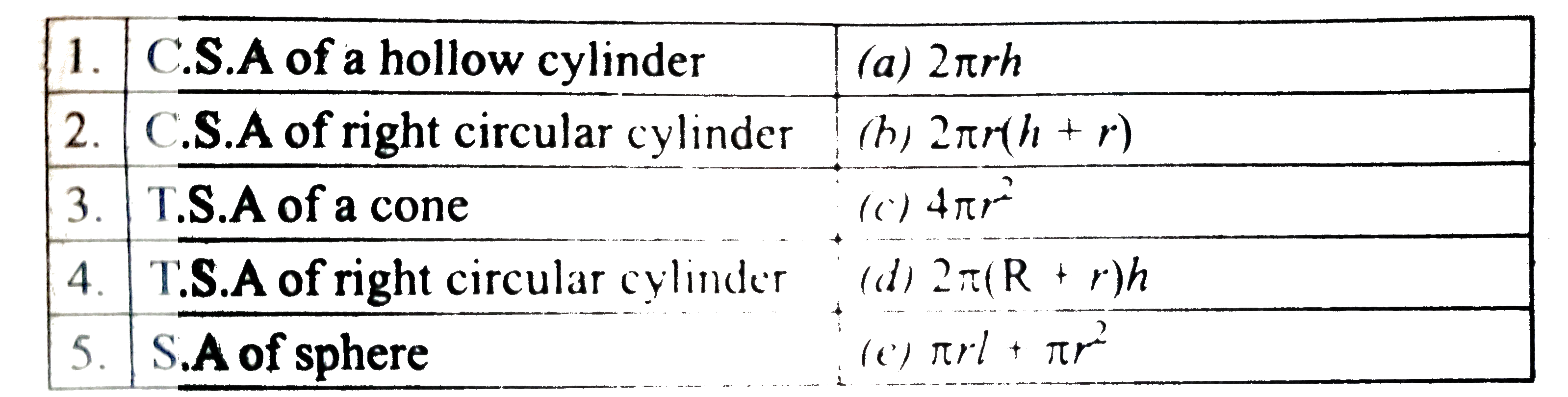
View SolutionTwo circles with centers O and O' of radii 6cm and 8cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle.The length of the common chord PQ is
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
Let the common chord be AB and Pand Q be the centers of the two circles.
AP=5cmand AQ=3cm.
PQ=4cm ...given
Now, segPQ⊥chordAB
AR=RB=12AB....perpendicular from center to the chord, bisects the chord
Let PR=xcm
so RQ=(4−x)cm
In△ARP,AP2=AR2+PR2
AR2=52−x2...(1)
In △ARQ,AQ2=AR2+QR2
AR2=32−(4−x)2...(2)
52−x2=32−(4−x)2...from (1) & (2)
25−x2=9−(16−8x+x2)
25−x2=−7+8x−x2
32=8x
x=4 substituting in equation(1) we get , AR2=25−16=9
AR=3cm
AB=2×AR=2×3=6
AB=6cmSo length of common chord is6 cm.
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionPQ is a chord of the circle with centre at O. Draw two tangents at P and Q respectively .
View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
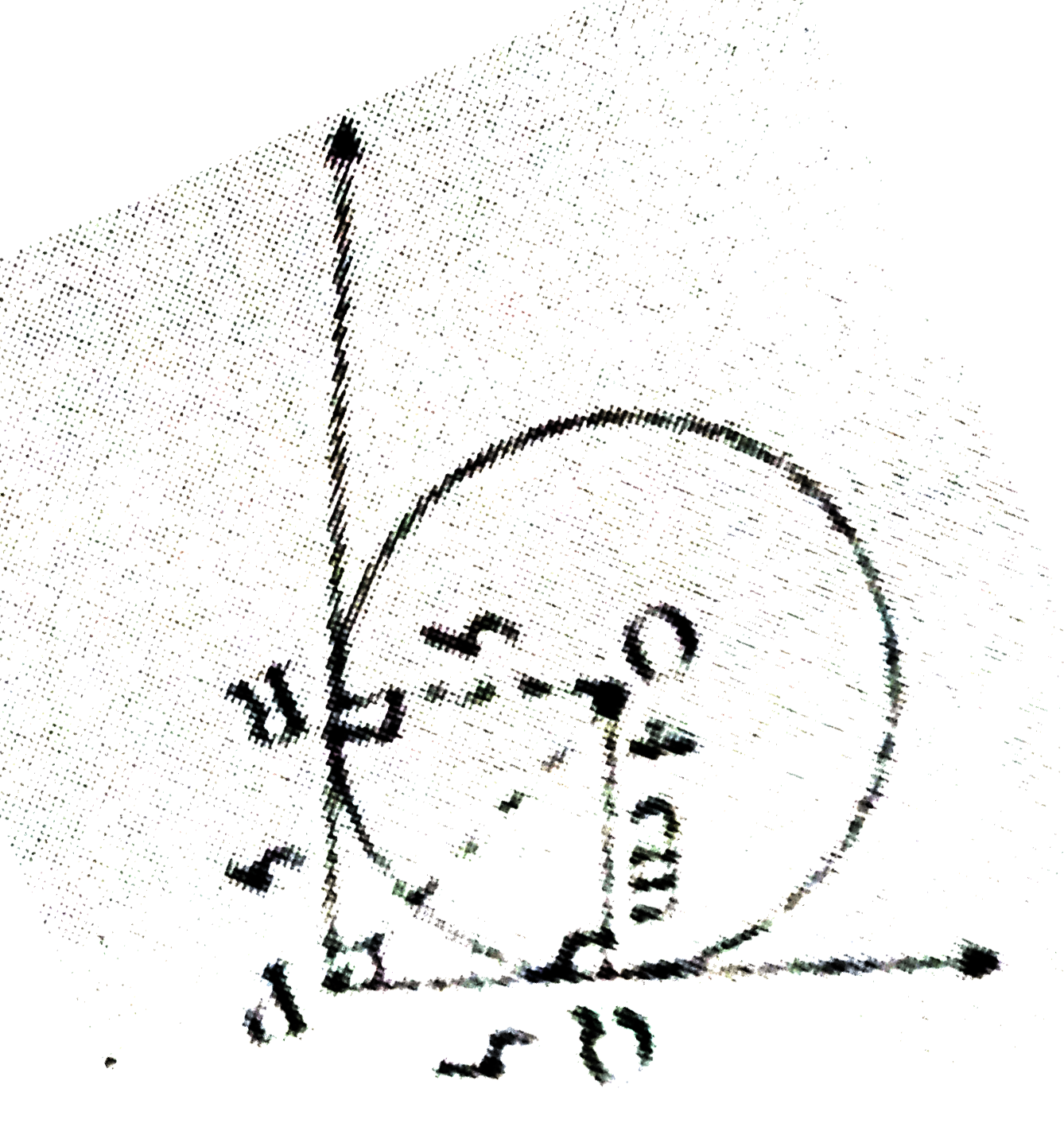
View SolutionTwo circles with centres O and O' of radii 3cm and 4 cm, respectively intersect at two points P and Q, such that OP and O' P are tangents to the two circles. Find the length of the common chord PQ.
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm , respectively intersect at two points P and Q such that OP and O'P are tangents to the two circle . Find the length of the common chord PQ.
View SolutionTwo circles with centers O and O' of radii 6cm and 8 cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle. The length of the common chord PQ is
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionTwo circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
View Solution
