Two solid cones A and B are placed in a cylindrical tube as shown in the figure The ratio of their capacities is 2:1 Find the heights and capacities of cones Also find the volume of the remaining portion of the cylinder. 21 cm

Video Solution

Text Solution

Verified by Experts

Let volume of cone A be 2 V and volume of cone B be V .Again, let height of the cone $A = h_{1}$
cm, then height of cone $B = (21 - h_{1}) c m$

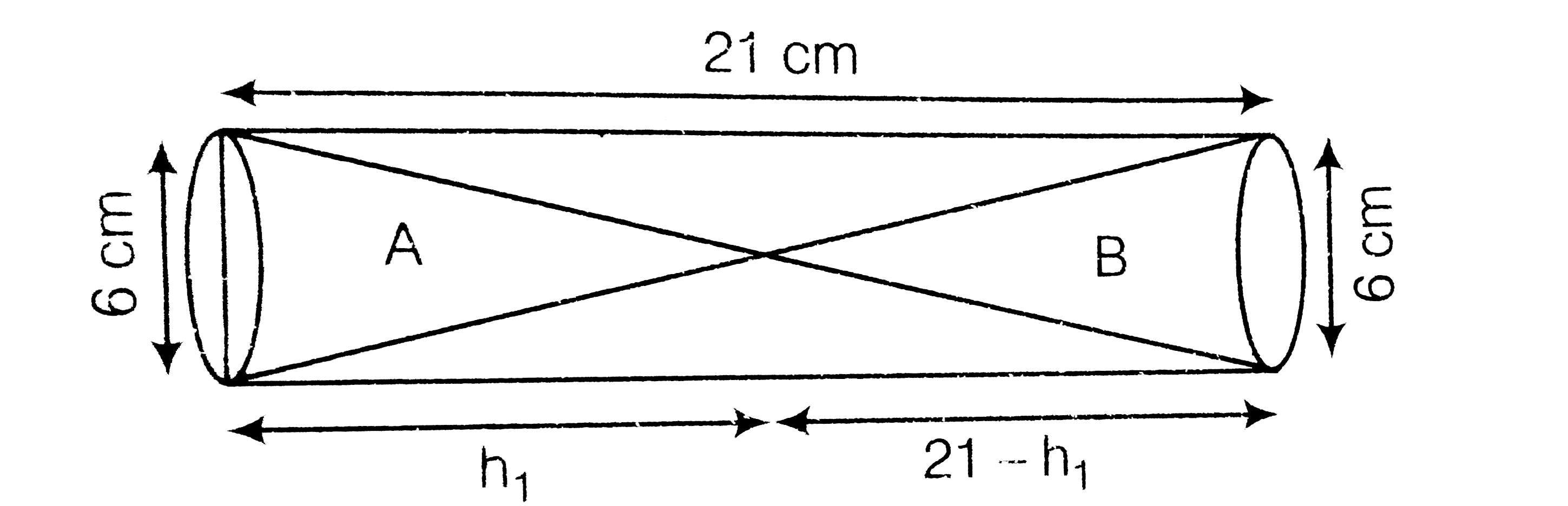
Given, diameter of the cone = 6 cm
$∴$ Radius of the cone $= \frac{6}{2} = 3 c m$
Now, volume of the cone , $A = 2 V = \frac{1}{3} π r^{2} h = \frac{1}{3} π {(3)}^{2} h_{1}$
$\Rightarrow V = \frac{1}{6} π 9 h_{1} = \frac{3}{2} π {(3)}^{2} h_{1}$
and volume of the cone , $B = V = \frac{1}{{(3)}^{2}} (21 - h_{1}) = 3 π (21 - h_{1})$
From Eqs. (i ) and (ii) ,
$\frac{3}{2} h_{1} π = 3 π (21 - h_{1})$
$\Rightarrow h_{1} = 2 (21 - h_{1})$
$\Rightarrow 3 h_{1} = 42$
$\Rightarrow h_{1} = \frac{42}{3} = 14 c m$
$∴$ " "Height of cone , $B = 21 - h_{1} = 21 - 14 = 7 c m$
Now, " " volume of the cone , $A = 3 \times 14 \times \frac{22}{7} = 132 c m^{3} [Using Eq. (i)]$
and $Volume of the cylinder = π r^{2} h = \frac{22}{7} \times 9 \times 7 = 66 c m^{3} [Using Eq.(ii)]$
Now, $volume of the cylinder = π r^{2} h = \frac{22}{7} {(3)}^{2} \times 21 = 594 c m^{3}$
$∴$ Required volume of the remaining portion = volume of the cylinder - (Volume of cone A + Volume of cone B)
$= 594 - (132 + 66)$
$= 396 c m^{3}$

Updated on:21/07/2023

The radius of the base of a cone is 21 cm and the height is 20 cm. Find the volume the cone
A $8460 c m^{3}$
B $9240 c m^{3}$
C $4620 c m^{3}$
D $3230 c m^{3}$
The ratio of heights of 2 cones is 3 : 4 and the ratio of radius of 2 cones is 5 : 6 . Find the ratio of volume of 2 cones.
A75/144
B75/72
C72/75
D144/75