Using mean value theorem, prove that for all
Video Solution
Text Solution
Mean value theorem states that if a function is continuous and differentiable in interval , then,
, where c lies in .
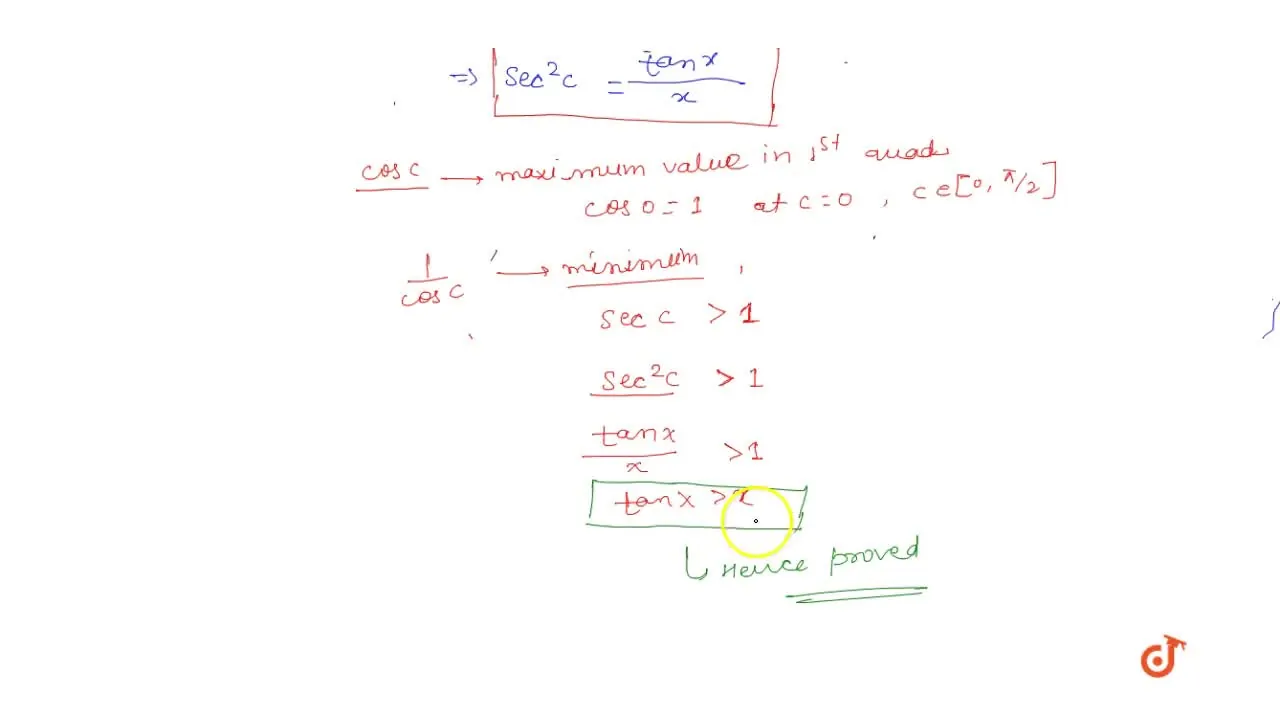
Let where .
Then, from Lagranges Mean value theorem,
If we apply Mean value theorem on .
Then,
Here,
From (1),
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Using mean value theorem, prove that tanx>x for all x(0,π2).
View SolutionProve that tanx>x for all x∈[0,π2]
View SolutionUsing Lagranges mean value theorem, show that sin⟨xforx⟩0.
View SolutionUsing LMVT prove that tanx>x in (0,π2),
View SolutionUsing Lagrange's mean value theorem prove that if b>a>0
then b−a1+b2<tan−1b−tan−1a<b−a1+a2View SolutionProve that tanx>x+x33 for all x∈(0,π2).
View SolutionProve that 2sinx+tanx≥3x, for all x∈[0,π2].
View SolutionUse the mean value theorem to prove ex≥1+x∀x∈R
View SolutionUsing Lagranges mean value theorem, prove that |cosa−cosb|≤|a−b|.
View SolutionUsing intermediate value theorem, prove that there exists a number x such that x2005+11+sin2x=2005.
View Solution