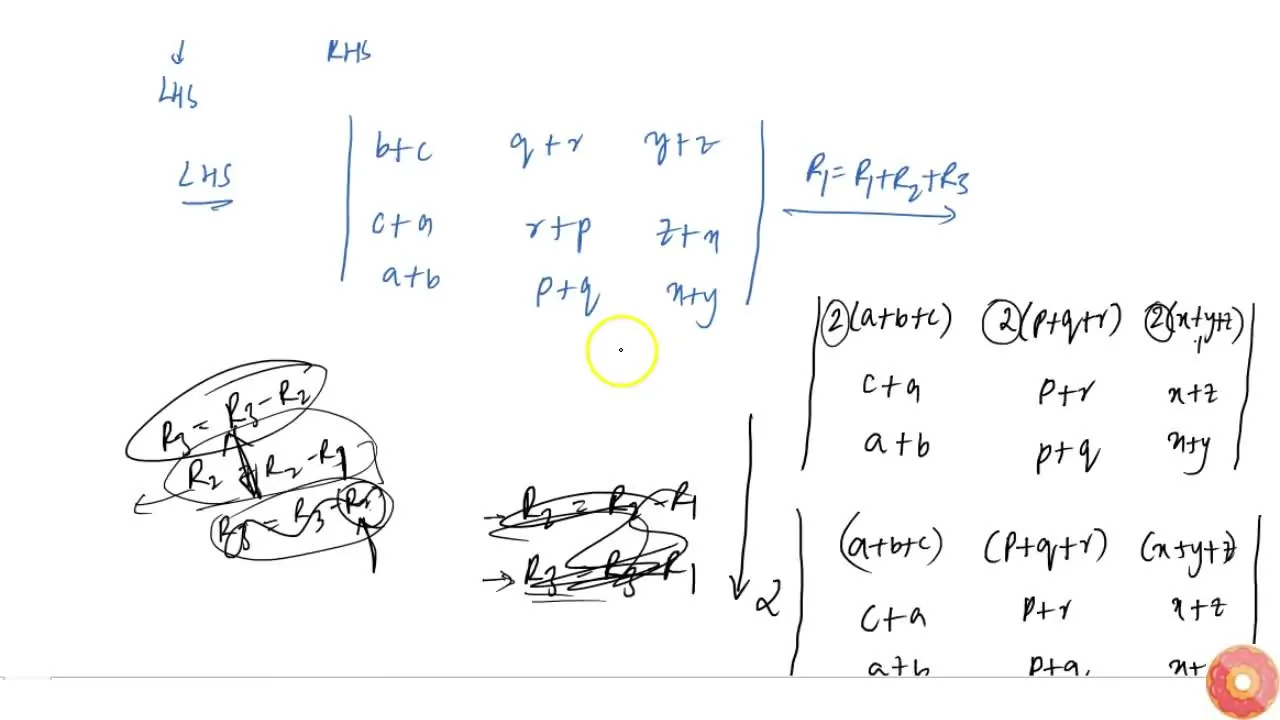
Using properties of determinants, prove that ∣∣ ∣ ∣∣b+cq+ry+zc+ar+pz+xc+bp+qx+y∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣apxbqycrz∣∣ ∣ ∣∣
L.H.S.=∣∣
∣
∣∣b+cq+ry+zc+ar+pz+xa+bp+qx+y∣∣
∣
∣∣
Applying R1→R1+R2+R3
=∣∣
∣
∣∣2(a+b+c)2(p+q+r)2(x+y+z)c+ar+pz+xa+bp+qx+y∣∣
∣
∣∣
=2∣∣
∣
∣∣a+b+cp+q+rx+y+zc+ar+pz+xa+bp+qx+y∣∣
∣
∣∣
Applying R2→R2−R1 and R3→R3−R1
=2∣∣
∣
∣∣a+b+cp+q+rx+y+z−b−q−y−c−r−z∣∣
∣
∣∣
Applying R1→R1+R2+R3
=2∣∣
∣
∣∣apx−b−q−y−c−r−z∣∣
∣
∣∣
=2(−1)(−1)∣∣
∣
∣∣apxbqycrz∣∣
∣
∣∣
=2∣∣
∣
∣∣apxbqycrz∣∣
∣
∣∣=R.H.S.
Related Playlists
Similar Questions
Use the properties of determinant and without expanding prove that ∣∣ ∣ ∣∣b+cq+ry+zc+ar+pz+xa+bp+qx+y∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣apxbqycrz∣∣ ∣ ∣∣.
View SolutionUsing the properties of determinats, prove that
∣∣ ∣ ∣ ∣ ∣∣(a+b)2ccca(b+c)2aabb(c+a)2b∣∣ ∣ ∣ ∣ ∣∣=2(a+b+c)3.
Or, If p≠0,q≠0and∣∣ ∣ ∣∣pqpα+qqrqα+rpα+qqα+r0∣∣ ∣ ∣∣=0 then using the propetries of eterminants, prove that at least one of the following statements is true:
(a) p,q,r are in GP (b) α is a root of the equation px2+2qx+r=0.View SolutionUsing the property of determinants and without expanding, prove that:∣∣ ∣ ∣∣b+cq+ry+zc+ar+pz+xa+bp+qx+y∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣apxbqycrz∣∣ ∣ ∣∣
View SolutionProve that: ∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣=∣∣ ∣ ∣∣ybqxapzcr∣∣ ∣ ∣∣
View SolutionWithout expansion, prove the following: ∣∣ ∣ ∣∣a+bb+cc+ap+qq+rr+px+yy+zz+x∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣abcpqrxyz∣∣ ∣ ∣∣
View SolutionWithout expanding, prove that :
∣∣ ∣ ∣ ∣∣1+bb+cc+ap+qq+rr+px+yy+zz+xx+yy+zz+x∣∣ ∣ ∣ ∣∣=2∣∣ ∣ ∣∣abcpqrxyz∣∣ ∣ ∣∣View SolutionUsing the property of determinants and without expanding in questions 1 to 7 prove that ,
∣∣ ∣ ∣∣xax+ayby+bzcz+c∣∣ ∣ ∣∣=0View SolutionProve that: ∣∣ ∣ ∣∣b+cc+aa+bq+rr+pp+qy+zz+xx+y∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣abcpqrxyz∣∣ ∣ ∣∣
View SolutionIf A=∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣andB=∣∣ ∣ ∣∣q−by−pa−xr−cz∣∣ ∣ ∣∣, then
View SolutionWithout expanding, prove that |abcxyzpqr|=|xyzpqrabc|=|ybqxapzcr|
View Solution