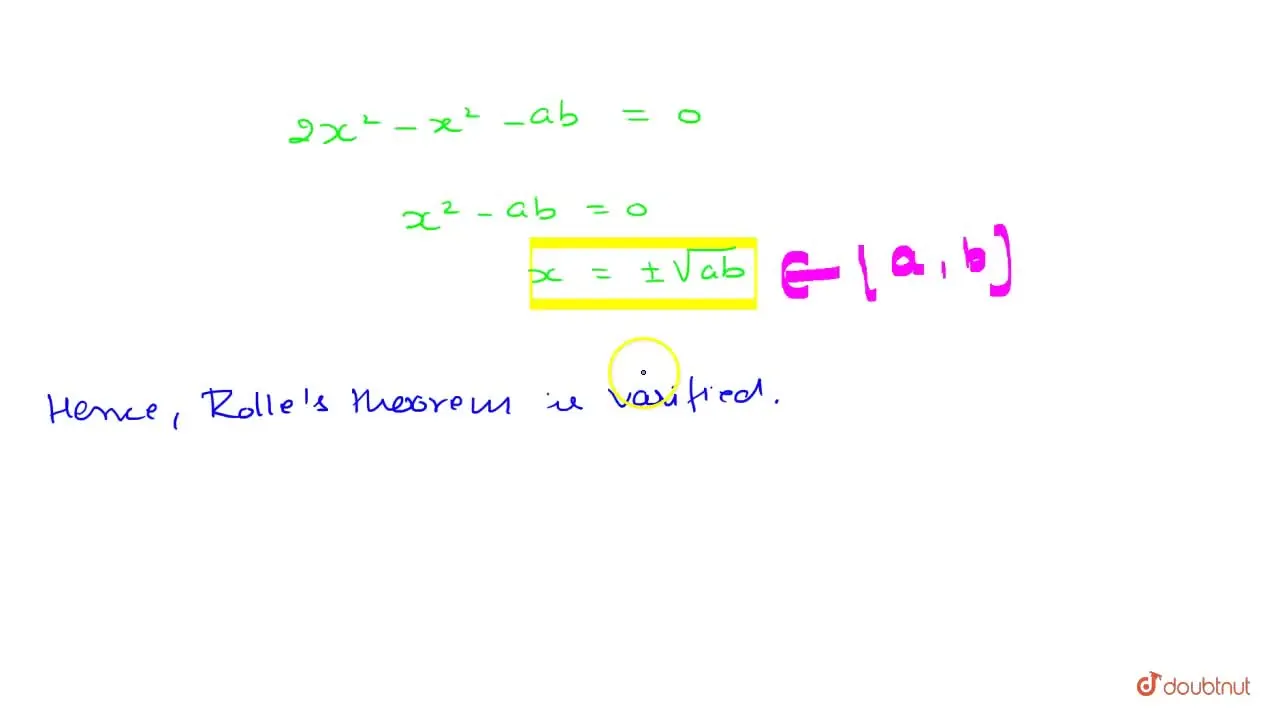Verify Rolle's theorem for the following functions
(i) f(x)=√4−x2 in [−2,2]
(ii) f(x)=log(x2+ab(a+b)x] in [a,b], where 0<a<b
(i) Consider f(x)=√4−x2 in [−2,2]
Clearly , f(x)=√4−x2 has a unique and definite value for each x∈[−2,2]. So, at each point of [−2,2], the limit is equal to the value of the function.
∴f(x) is continuous on [−2,2]
Also, f'(x)=−x√4−x2, which clearly exists for each x∈[−2,2]
So, f(x) is differentiable on [−2,2]
Alos, f(−2)=f(2)=0
Thus, all the conditions of Rolle's theorem are satisfied.
so, there must exist c∈[−2,2]such that f'(c)=0
Now, f'(c)=0⇔−c√4−c2=0⇔c=0
Thus, c=0⇔[−2,2]such that f'(c)=0
Hence, Rolle's theorem is verified.
(ii) Consider
f(x)=log[x2+ab(a+b)x]=log(x2+ab)−log(a+b)−logx.
Clearly, f(x) has a unique and definite value for each x∈[a,b], where 0<a<x<b.
So, the value of the function is equal to the limit of the function at each point of [a,b]
∴f(x) is continuous on [a, b]
Also, f'(x)=[2x(x2+ab)−1x], which is clearly definite and finite for all values of x in [a, b]
So, f(x) is differentiable on [a,b]. Moreover, f(a)=f(b)=0
Thus, all the conditions of Rolle's theorem are satisfied.
So, there must exist c∈]a,b[ such that f'(c)=0
But, f'(c)=0⇔2c(c2+ab)−1c=0
⇔(c2−ab)c(c2+ab)=0⇔c2−ab=0⇔c=√ab.
Now, c being the geometric mean of a and b, it follows that a<c<b.
Thus, c∈[a,b]such that f'(c)=0
Hence, Rolle's theorem is verified.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11A21videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11B17videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 737videos
ADJOINT AND INVERSE OF A MATRIX
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
Similar Questions
Verify Rolle's theorem for each of the following functions :
f(x)=√1−x2 in [−1,1]View SolutionVerify Rolle's theorem for the following function f(x)=2x3+x2−4x−2
View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=(x−1)(x−2)2 in [1,2]View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=x2−x−12 in [−3,4]View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=x2−5x+6 in [2,3]View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=cos2x in [0,π]View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=sinx−sin2x in [0,2π]View SolutionVerify the truth of Rolle's Theorem for the following functions
f(x)=√x−2 in [1,2]View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=x(x+2)exin [−2,1]View SolutionVerify Rolle's theorem for each of the following functions :
f(x)=x2−4x+3 in [1,3]View Solution