Volume of prism
Prism
In this article, we will focus on prism. Students would also be able to learn about the volume of the prism. We would also work on the examples of the prism where it would make things quite clear to you.
What is Prism?
The three-dimensional solid object whose two ends are exactly of the same shape is the prism. It is the combination of the identical bases, flat faces and same cross-sections. Without the bases, the faces are parallelograms. In case you wish to take the cross-section or the prism parallel to the base, then you would find that the cross-sections would look like the bases.
What is the shape of the prism?
A prism has got a solid shape where it consists of two equal ends as well as identical cross-section and flat faces or surfaces. It is also called triangular prism as the cross-section looks like a triangle. The shape of the prism does not have any curve. Therefore, it should be kept in mind that a prism can be rectangular, cubic, pentagonal as well as other polygon shapes, excluding the circular shape.
What are the types of prisms?
Based on the cross-sections, the prisms are of two types which are Regular Prism and Irregular Prism. We will have a look at these types of prisms as below:
- Regular Prism: A regular prism is the one where the bases of the prism are in the shape of a regular polygon.
- Irregular Prism: An irregular prism has the base in the shape of an irregular polygon.
The classification of the prism can be further done into two types which are Right Prism and Oblique Prism
- Right Prism: Right prism is the one whose faces and the joining edges are perpendicular to the base faces. Here the side faces are rectangle.
- Oblique Prism: In this type of prism, the faces and the joining edges are not perpendicular to the base faces. The side faces are parallelograms.
Based on the shape of the bases, prisms are further classified as below:
- Rectangular
- Pentagonal
- Triangular
- Square
- Hexagonal
Prism Formulas
It is based on the surface area and volume of the prism for which the formulas are defined. It is because of the three-dimensional shape, the prism has both the properties, which are volume and surface area.
Surface Area of a Prism
The total area which is covered by the faces of the prism is the surface area of the prism.
So, the formula of the Surface Area of a Prism = 2(Base Area) + (Base perimeter × length)
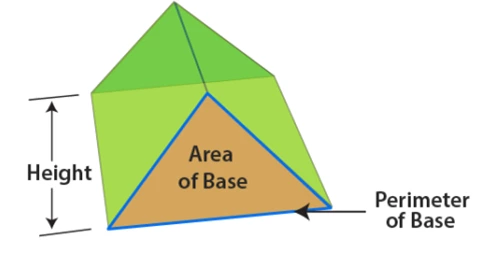
What is the Volume of a Prism?
The total space which is occupied by the three-dimensional object is called the volume of a prism. So, in math, it is the product of the area of the base and the length.
Therefore, the volume of a Prism = Base Area × Length
Volume of a Prism Formula
Now, we will discuss the formula of the volume of a prism. Here, we will concentrate on the rectangular prism, triangular prism, pentagonal prism, and so on.
Volume of a Rectangular prism
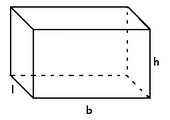
There are four rectangular faces and two parallel rectangular bases in a rectangular prism. The rectangular prism is also called “Cuboid”.
So, the volume of a Rectangular Prism = lbh cubic units.
Here,
l = Base width of a rectangular prism
b = Base length of a rectangular prism
h = height of a rectangular prism
Volume of a Triangular Prism
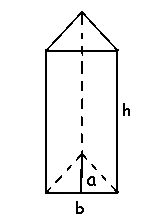
A triangular prism has got three rectangular faces and two triangular bases. The formula for the volume of a triangular prism is given as:
The volume of a Triangular Prism = (½) abh cubic units.
Here
a = Apothem length of a triangular prism
b = Base length of a triangular prism
h = height of a triangular prism
Volume of a Pentagonal Prism
There are five rectangular faces and two parallel pentagonal bases in a Pentagonal Prism.
So, the Volume of a Pentagonal Prism = (5/2) abh cubic units
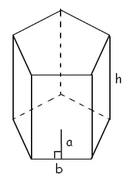
Here,
a = Apothem length of the pentagonal prism.
b = Base length of the pentagonal prism.
h = Height of the pentagonal prism
Volume of a Hexagonal Prism
There are six rectangular faces and two parallel hexagonal bases in a hexagonal prism.
The volume of a Hexagonal Prism = 3abh cubic units
Here,
a = Apothem length of the hexagonal prism.
b = Base length of the hexagonal prism.
h = Height of the hexagonal prism.
Related Videos:
- Area and Perimeter of rectangle
- Area and Perimeter of square
- Area and Perimeter of triangle
- Area and Perimeter of trapezium
- Area and Perimeter of rhombus
- Area and Perimeter of circle
We will concentrate on some of the examples of prism to get some good understanding about it.
Example 1: The area of a triangular prism is 50 cm2 and height is 8 cm? Can you find the volume?
Solution: Given,
Area = 50 cm2
Height = 8 cm
We are familiar that,
(V) volume of a prism = Base area × Height cubic units
So, V = 50 × 8 = 400
Therefore, the volume of a triangular prism = 400 cm3.
Example 2: The volume of a square is 400 cm3 and the base area is 80 cm2? Can you calculate its height?
Solution: Given,
The volume of a square prism = 400cm3
Base Area = 80cm2
Now by calculating the height of the square prism, we get,
The volume of square prism = Base area × height
400 = 80 × prism height
So, the height, h = 400/80
So, the height of the prism, h = 5 cm.
Example 3: A right prism has a height of 12 cm. It stands on a base which is a regular hexagon. The area of the whole surface of the prism is 1152√3 sq.cm. Can you find the volume of the prism?
Solution: Let us take 'a' be the length of a side of the regular hexagon. Here, the area of its base = area of the regular hexagon and the area of side-faces of the prism
= 6a . 12 sq. cm. sq. cm. and
= (6a²/4) cot (π/4), [since, the area of a regular polygon of n sides = (na²)/4 cot (π/5)]
= {(3√3)/2}a² sq,. cm.
According to problem, the area of the whole surface of the prism = 1152√3
Therefore, 6a ∙ 12 + 2 ∙ {(3√3)/2}a² = 1152√3
Or, a² + 8√3 a - 384 = 0
Or, a² + 16√3 a - 8√3 a - 384 = 0
Or, a(a + 16√3) – 8√3 (a + 16√3 a) = 0
Or, (a + 16√3 a)(a - 8√3) = 0
Therefore, either, a = - 16√3 or, a = 8√3
Since a is positive , the value of a = -16√3 is admissible.
Therefore, we take a = 8√3
Therefore, the required volume of the prism
= area of its base × its height
= (3√3)/2 ∙ (8√3)² ∙ 12 c.c.
= 3456√3 c.c.
Example 4: The area of a triangular prism is 40 cm2 and height is 6 cm? Can you find the volume?
Solution: Given,
Area of prism = 40 cm2
Height = 6 cm
We are familiar that,
(V) volume of a prism = Base area × Height cubic units
So, V = 60 × 4 = 240
Therefore, the volume of a triangular prism = 240 cm3.
Important Chapters:





Similar Questions
Knowledge Check
The base of a right prism an equilateral triangle of side 8cm and height of the prism is 10 cm. Then the volume of the prism is
A320√3 cubic cmB160√3 cubic cmC150√3 cubic cmD300√3 cubic cmThe base of a prism is a regular hexagon. If every edge of the prism measures 1 m, then the volume of the prism is :
A3√22m3B3√32m3C6√25m3D5√32m3The base of a prism is a regular hexagon. If every edge of the prism measures 1 m, then the volume of the prism is :
A3√22m3B3√32m3C6√25m3D5√32m3
The base of a right prism is a square having side of 10 cm. If its height is 8 cm , then find the total surface area and volume of the prism .
View SolutionThe height of a right prism is 10 cm. Its base is a triangle with sides 10 cm,17 cm and 9 cm. Find the volume of the prism.
View SolutionThe base of a right prism is a square of perimeter 20 cm and its height is 30 cm. What is the volume of the prism?
View SolutionThe base of a right prism is an equilateral triangle of edge 12 m. If the volume of the volume of the prism is 288√3m3, then its height is ________.
View SolutionThe perimeter of the triangular base of a right prism is 15 cm and radius of the incircle of the triangular base is 3 cm. If the volume of the prism be 270cm3, then the height of the prism is –
View Solution

