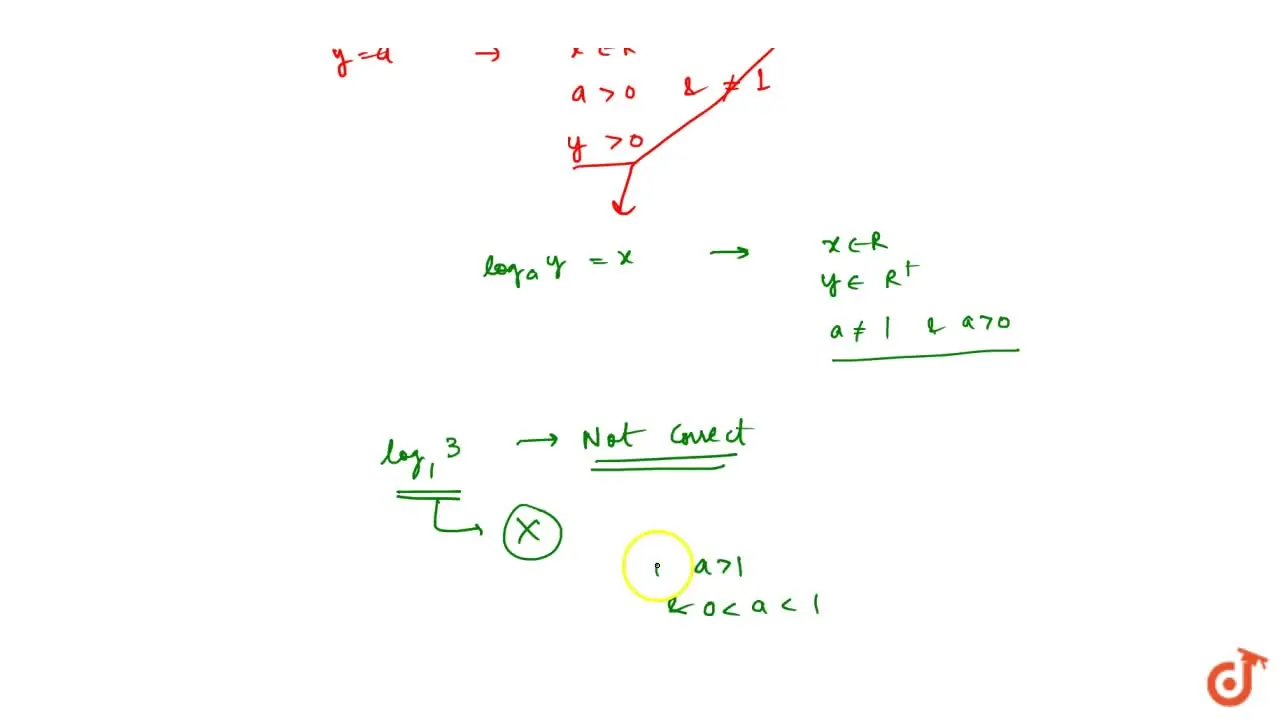
What is logarithmic function ?
Video Solution
|
Answer
Step by step video & image solution for What is logarithmic function ? by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023
Similar Questions
Prove that the logarithmic function is strictly increasing on (0,∞).
View SolutionWhat is Logarithmic equation ?
View SolutionDerivatives of exponential and logarithmic functions
View SolutionGraph of Logarithmic function when base>1
View SolutionGraph of Logarithmic function when 0<base<1
View SolutionDerivative OF logarithmic functions, theory as well as questions
View SolutionThe logarithmic function defined as f(x) =log x is strictly increasing in :
View SolutionGeneral Properties of Logarithmic Function
View SolutionA logarithmic function is continuous in its domain.
View SolutionProblems on Introduction to Logarithmic Function
View Solution