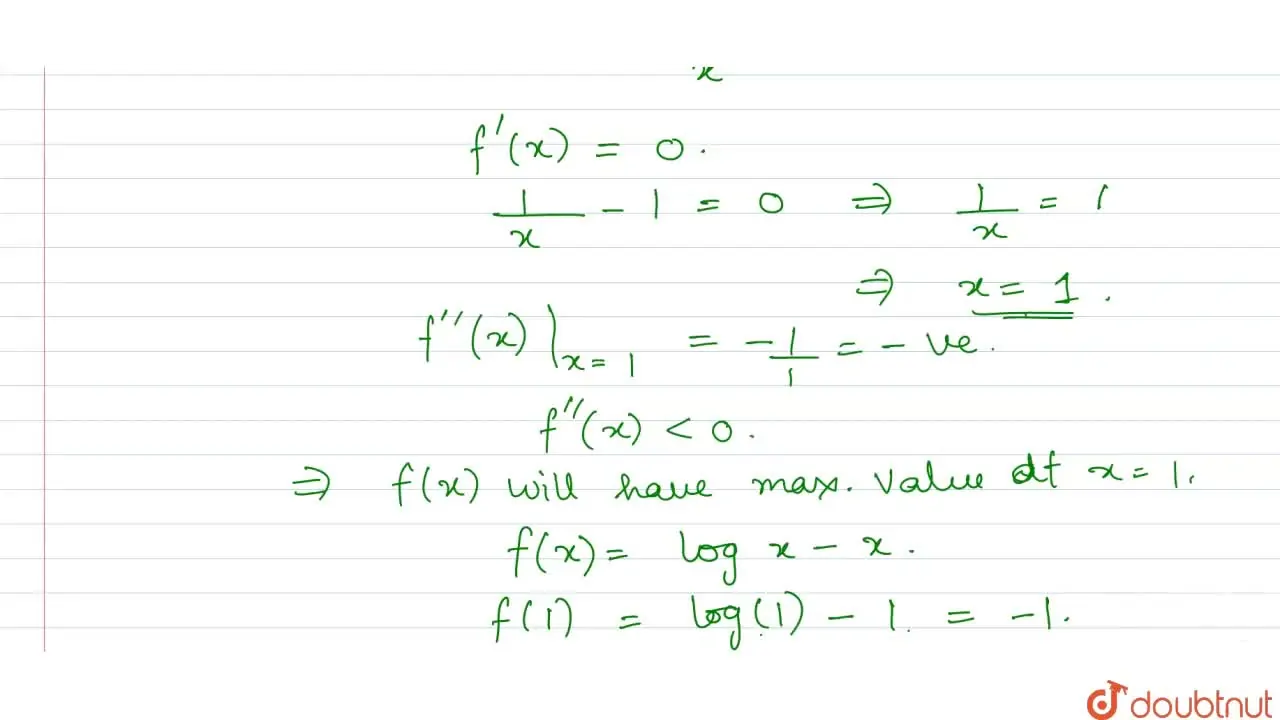What is the maximum value of the function logx-x?
A
−1
B
0
C
1
D
∞
Video Solution
Text Solution
The correct Answer is:A
Let y = log x -x
∴dydx=1x−1andd2ydx2=−1x2
For maximum and minumum value of y
dydx=1x−1=0→1x=1→x=1
Forx=1,d2ydx2=−ve
Thus the value of given function is maximum for x=1
So the maximum value of hte function =log (1)-1 =-1
|
Updated on:21/07/2023
Related Playlists
Similar Questions
What is the maximum value of ihe function log x -x?
View SolutionConsider the function f(x)=x2−x+1x2+x+1
What is the maximum value of the function ?View SolutionConsider the function f(x)=0.75x4−x3−9x2+7 What is the maximum value of the function ?
View SolutionThe maximum value of the function is
View SolutionWhat is the maximum value of the function sinx+cosx?
View SolutionConsider the function f(X)=x2−x+1x2+x+1
What is the maximum value of the fucnction ?View SolutionConsider the function f(x)=0.75x4−x3−9x2+7
What is the maximum value of the function?View SolutionWhat is the maximum value of the function f(x)=4sin2x+1?
View Solution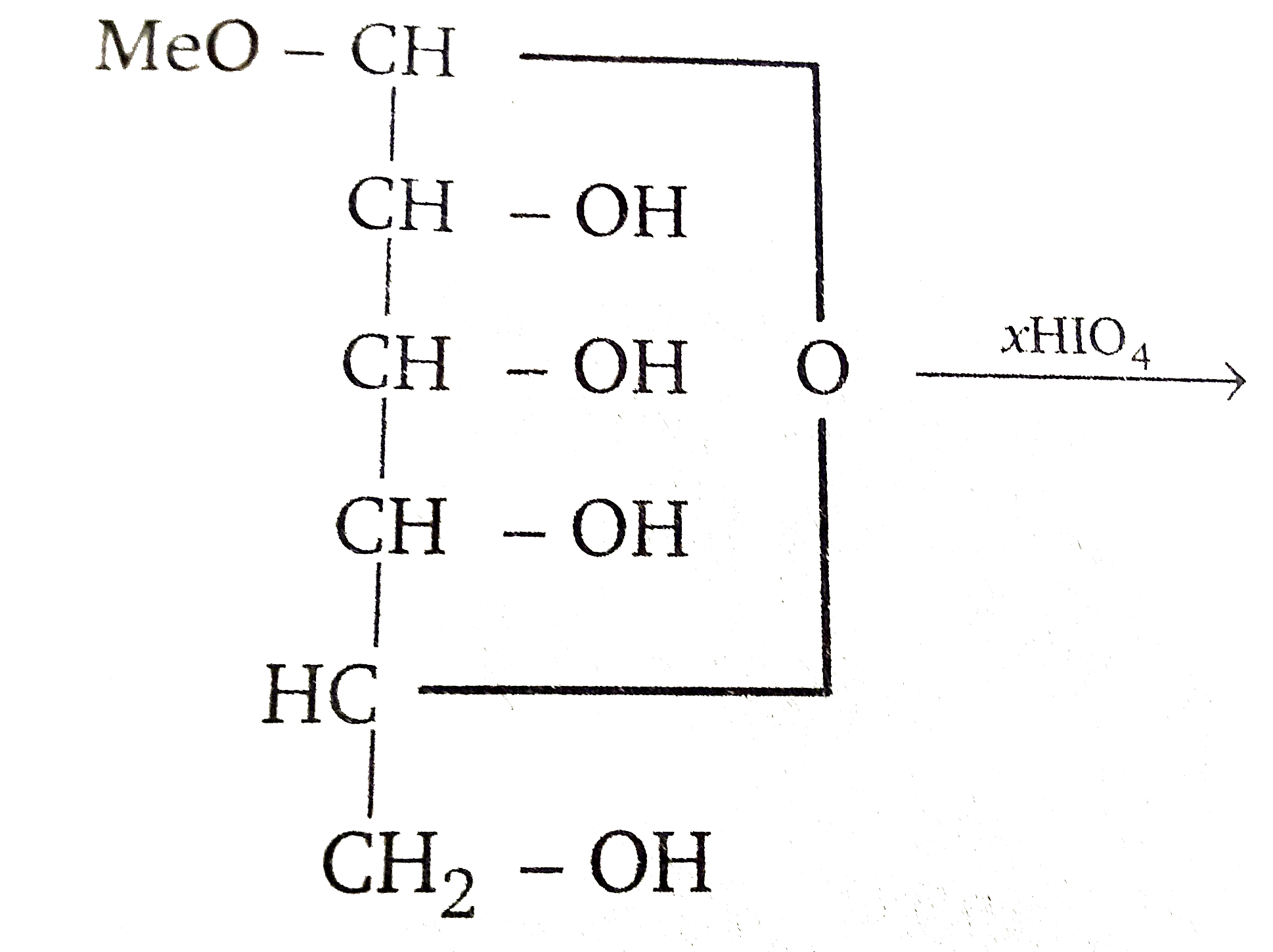 What is the maximum value of (x)?View Solution
What is the maximum value of (x)?View SolutionWhat is the maximum value of the function y = min (12−x,8+x)?
View Solution