Which of the following is not a criterion for congruence of triangle ?
SAS
ASA
SSA
SSS
The correct Answer is:C
To determine which of the following is not a criterion for the congruence of triangles, we need to analyze the options given: SAS, ASA, SSA, and SSS.
1. Understand the Criteria for Congruence of Triangles:
- SAS (Side-Angle-Side): Two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle. This is a valid criterion for congruence.
- ASA (Angle-Side-Angle): Two angles and the included side of one triangle are equal to two angles and the included side of another triangle. This is also a valid criterion for congruence.
- SSS (Side-Side-Side): All three sides of one triangle are equal to all three sides of another triangle. This is another valid criterion for congruence.
- SSA (Side-Side-Angle): Two sides and a non-included angle of one triangle are equal to two sides and a non-included angle of another triangle. This is not a valid criterion for congruence because it does not guarantee that the triangles are congruent.
2. Identify the Incorrect Option:
- From the analysis, we see that SAS, ASA, and SSS are valid criteria for triangle congruence, while SSA is not.
3. Conclusion:
- Therefore, the option that is not a criterion for congruence of triangles is SSA.
Final Answer:
The correct option is SSA.
- SAS (Side-Angle-Side): Two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle. This is a valid criterion for congruence.
- ASA (Angle-Side-Angle): Two angles and the included side of one triangle are equal to two angles and the included side of another triangle. This is also a valid criterion for congruence.
- SSS (Side-Side-Side): All three sides of one triangle are equal to all three sides of another triangle. This is another valid criterion for congruence.
- SSA (Side-Side-Angle): Two sides and a non-included angle of one triangle are equal to two sides and a non-included angle of another triangle. This is not a valid criterion for congruence because it does not guarantee that the triangles are congruent.
- From the analysis, we see that SAS, ASA, and SSS are valid criteria for triangle congruence, while SSA is not.
- Therefore, the option that is not a criterion for congruence of triangles is SSA.
The correct option is SSA.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
12 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS
11 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
- VOLUME AND SURFACE AREABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
Which of the following is not criterion for essentiality of an element?
ARequirement of the element is specificBNecessary for normal growth and reproductionCnot replaceable by another elementDindirectly involved in plant metabolismWhich of the following must be true?
(I) The area of triangle P.
(II) The area of triangle Q.
(III) The area of triangle R.
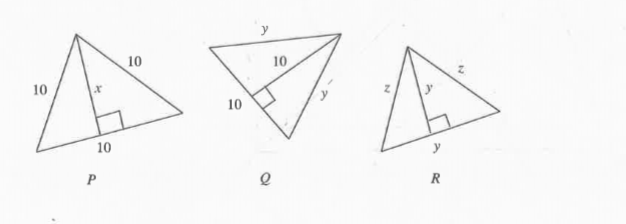 AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt II
AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt IIThe side lengths of a certain triangle are 4, 5, and 7 centrimeters. Which of the following descriptions best classifies this triangle?
AScalene acuteBScalene rightCScalene obtuseDIsosceles obtuse
Which of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In ΔABCandΔDEF, AB = DE, BC = EF and ∠B=∠E.
(b) In ΔABCandΔDEF,∠B=∠E=90∘, AC = DF and BC = EF.
(c) In ΔABCandΔQRP, AB = QR, ∠B=∠Rand∠C=∠P.
(d) In ΔABCandΔPQR, AB = PQ, AC = PR and BC = QR.
(e) In ΔABCandΔPQR, BC = QR, ∠A=90∘,∠C=∠R=40∘and∠Q=50∘.
View SolutionWhich of the following pairs of triangle are congruent by ASA condition?
View SolutionIn a triangle ABC, which of the following quantities denote the area of the triangles a2−b22sinAsinBsin(A−B)
View SolutionIf the area of △ABC is 21, and the length of the height minus the length of the base equals 1, which of the following is equal to the base of the triangle ?
View SolutionWhich one of the following is the true regarding the triangle shown in figure?
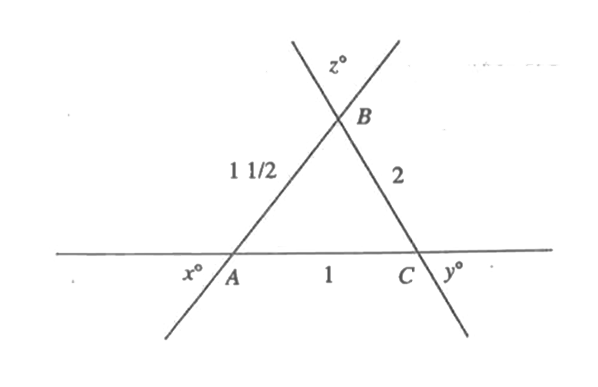
View Solution
