Complete Solutions to LEVEL - III of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| NARAYANA | LEVEL - III |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
A ray of light of intensity I is incident on a parallel glass slab at a point A as show. It undergoes partial reflection and refraction. At each reflaction `25%` of incident energy is reflected. The rays AB and A'B' undergo interference. The ratio `I_(max)//I_(min)` is
 02:00View Solution
02:00View SolutionTwo coherent sources of intensity ratio `beta` interfere, then `(I_(max)-I_(min))/(I_(max)+I_(min))` is
03:58View SolutionMonochromatic green light of wavelength 550 nm illuminates two parallel narrow slits `7.7mu m` apart. The angular deviation `theta` of third order (for m =3) bright fringe in radian and in degree
04:22View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
08:33View SolutionIn the Young's double slit experiment, maximum of bright bands observed (inclusive of the central bright band) is found to be 11. If `lambda` is the wavelength of the monochromatic light used, the distance between the slits is
03:28View SolutionIn a double slit experiment, interference is obtained from electron waves produced in an electron gun supplied with voltage V. If `lambda` is wavelength of the beam, D is the distance of screen, d is the spacing between coherent source, h is Planck's constant, e is charge on electron and m is mass of electron, then fringe width is given as
03:09View SolutionTwo identical narrow slits `S_(1)` and `S_(2)` are illuminated by light of wavelength `lambda` from a point source P. If, as shown in the diagtam above the light is then allowed to fall on a scree, and if n is a positive integer, the condition for destructive interference at Q is that
 02:43View Solution
02:43View SolutionFig, here shows P and Q as two equally intense coherent sources emitting radiations of wavelength 20m. The separation PQ si 5m, and phase of P is ahead of the phase Q by `90^(@)`. A, B and C are three distant points ofobservation equidistant from the mid - point of PQ. The intensity of radiations of A, B, C will beasr the ratio
 08:16View Solution
08:16View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength `lambda`. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of `n=4` interference maxima is given as
 02:54View Solution
02:54View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is `lambda` and I is theintensity of central bright fringe, then intensity at distance from central maximum is
04:00View SolutionThe polaroids are placed in the path of unpolarized beam of intensity `I_(0)` such that no light is emitted fromthesecond polarid. If a third polaroid whose polarization axis makes an angle `theta` with the polarization axis of first polaroid, is placed between these4 polariods then the intensity of light emerging from the last polariod will be
05:08View SolutionTwo coherent point sources `S_(1)` and `S_(2)` vibrating in phase emit light of wavelength `lambda`. The separation between the sources is `2lambda`. Consider a line passing through `S_(2)` and perpendicular to line `S_(1) S_(2)`. Find the position of farthest and nearest minima.
 .11:59View Solution
.11:59View SolutionIn YDSE, let A and B be two slits. Films of thickness `t_(A)` and `t_(B)` and refractive `mu_(A)` and `mu_(B)` are placed in front of A and B, respectively. If `mu_(A) t_(A) = mu_(A) t_(B)`, then the central maxima will
03:38View SolutionA monochromatic beam of light is used for the formation of fringes on a screen by illuminating the twoslits in the Young,s double slit interfrence experiment. When a thin film of mic is interposed in the path of one of the interfering beams
03:51View SolutionWhat happens to the fringe pattern when the Young's double slit experiment is performed in water intesed of air ?
04:23View SolutionTwo periodic waves of intensities `I_(1)` and `I_(2)` pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:
04:16View SolutionWhat is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film `=1.5,` wavelength of the lilght incident on the film `=600` nm.03:34View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at separation x `(lt lt R)` symmetrical about the center of the circle. The sources emit identical wavelength `lambda` each. The number of points on the circle of maximum intensity is `(x = 5 lambda)`
04:45View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index `n_(1)`. The wavelength of light in this medium is `lambda_(1)`. A transparent of thickness t and refractive index `n_(3)` is put in front of one slit. The medium between the screen and the plane of the slits is `n_(2)`. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
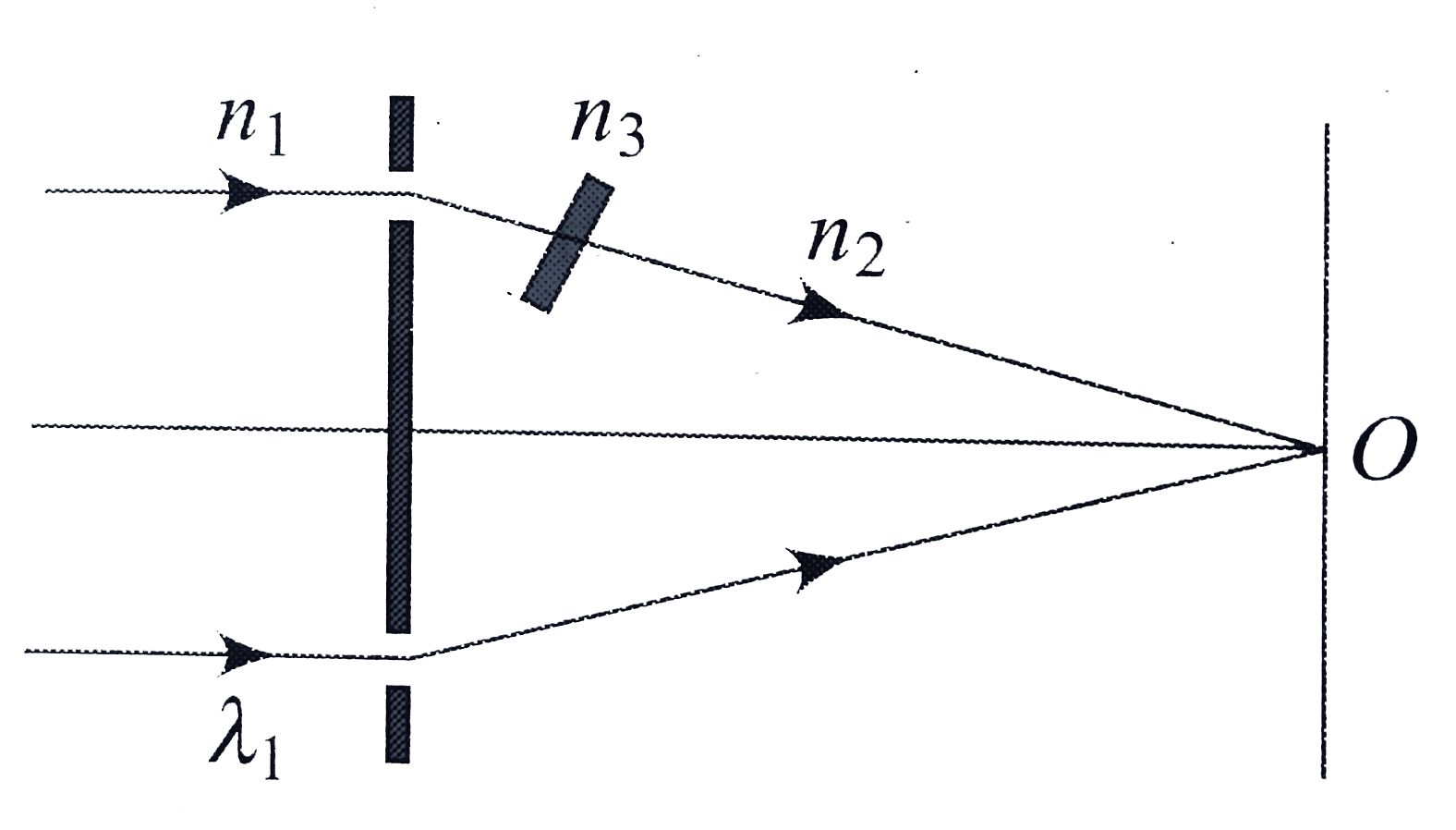 03:23View Solution
03:23View SolutionIn Young's double slit experiment, the 10th bright fringe is at a distance x from the central fringe. Then
a) the 10th dark fringe is at a distance of `19x//20` from the central fringe
b) the 10th dark fringe is at a distance of `21x//20` from the central fringe
c) the 5th dark fringe is at a distance of `x//2` from the central fringe.
d) the 5th dark fringe is at a distance of `9x//20` from the central fringe.04:45View SolutionIf `I_0` is the intensity of the principal maximum in the single slit diffraction pattern. Then what will be its intensity when the slit width is doubled?
03:01View SolutionLight of wavelength `6000 Å` from a distance source falls on a slit `0.5` mm wide. The distance between two dark bands on each side of the central bright band of the diffraction pattern observed on a screen placed at a distance 2m from the slit is
04:16View SolutionA parallel beam of wavelength `lambda=450xx10^9m` passes through a long slit of width `2xx10^-4m`. The angular divergence for which most of light is diffracted is
01:55View SolutionAssuming human pupil to have a radius of 0.25 cm and a comfortable viewing distance of 25 cm, the minimum separation between two objects than human eye can resolve at 500nm wavelength is :
02:38View SolutionThe box of a pin hole camera, of length L, has a hole of radius a . It is assumed that when the hole is illuminated by a parallel beam of light of wavelength `lamda` the spread of the spot (obtained on the opposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction. The spot would then have its minimum size (say b_(min)) when:
02:39View SolutionA polariser and an analyser are oriented so that the maximum amount of lights is transmmitted. Fraction of its maximum value is the intensity of the transmitted through reduced when the analyzer is rotated through (intensity of incident light `= I_(o)`) , a) `30^(@)` , b) `45^(@)` , c) `60^(@)`
05:11View SolutionAs polaroid examines two adjacent plane polarised beam A and B whose planes of polarisation are mutually perpendicular. In the first position of the analyser, beam B shows zero intensity. From this position a rotation `30^(@)` shows that thebeams have same intensity. The ratio of intensity of the two beam `I_(Z) & I_(B)`
05:25View SolutionAn analyser is inclined to a polariser at an angle of `30^(@)`. The intensity of light emerging on the polariser. Then n is equal to
03:37View SolutionWhen a beam of light wavelength `lambda` is incident on the surface of a liquid at an angle `phi` , the reflected ray in completely polarized. The wavelength og light in the liquid medium is
04:00View SolutionThe YDSE apparatus is modified by palcing an isotropic transperent plate of `mu = 1.5` and thinkness `t = 2 mu m` with tempatature coeffcient `2xx10^(-6) .^(@)C^(-1)` . A light of `6000 Å` units is incident. If the palte heated through a temperature `10 ^(@)C` then number of fringes will cross a particular point on the screen ? `(D =2m, d= 2mm)` .
07:07View Solution
LEVEL - III questions and complete solutions for chapter WAVE OPTICS of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS WAVE OPTICS
- C . U . Q (Diffraction light)
- C . U . Q (interference)
- C . U . Q (Polarisation)
- C . U . Q (Resolving power)
- C.U.Q
- Evaluate yourself - 1
- Evaluate yourself - 2
- Evaluate yourself - 3
- Example
- Exercise - 1 (C.W) Huygen. s principle
- Exercise - 1 (C.W) Interference
- Exercise - 1 (C.W) Diffraction
- Exercise - 1 (C.W) Resolving power
- Exercise - 1 (C.W) Polarisation
- Exercise - 1 (C.W) Diffraction
- Exercise - 1 (H.W) Diffraction
- Exercise - 1 (H.W) Interference
- Exercise - 1 (H.W) Polarisation
- Exercise - 1 (H.W) Resolving power
- Exercise - 2 (C . W) Diffraction
- Exercise - 2 (C . W) Polarisation
- Exercise - 2 (C . W) Resolving power
- Exercise - 2 (C . W) Interference
- Exercise - 2 (H. W) Diffraction
- Exercise - 2 (H. W) Interference
- Exercise - 2 (H. W) Polarisation
- Exercise - 3
- Exercise - 4 Diffraction
- Exercise - 4 Interference of light
- Exercise - 4 Polarisation
- Exercise -1 (C.W) Diffraction
- Exercise -1 (C.W) Resolving power
- Exercise -1 (C.W) Huygen. s principle
- Exercise -1 (C.W) Huygen. s principle
- LEVEL - I (C.W)
- LEVEL - I(H.W)
- LEVEL - II (C.W)
- LEVEL - II(H.W)
- LEVEL - III
- LEVEL - V
- LEVEL - VI
- NCERT Based Questions
