INTRODUCTION TO TRIGONOMETRY for Class 10 MATHS

To bachcho apne triangles ke baare mein to apni pichli classes mein padha hai, particularly right triangle ke baare mein chahe fir wo similarity of triangle ho yaa Pythagoras theorem etc.
Es chapter mein hum triangle ki side and angle ke beech mein relationship smjhenge. Bachcho sabse pehle hum ye dekhte hai ki why we are studying this chapter ? Isko samjhne ke liye chalo apne surroundings se hum kuch live examples lete hai. Manlo aap apne friends ke sath delhi ghumne gye aur Qutub Minar pahuch gye, Ab aapko Qutub Minar ki height nikalni hai to aap kaise nikalenge ?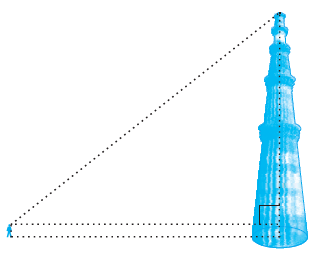


Chalo ek aur situation consider karte hai manlo apne ek hot air balloon dekha aur jaise hi apne usko dekha aap apni mom ko dikhane ke liye bula ke late ho aur itni der mein balloon position $A$ se $B$ pe aa gya. To kya aap balloon $B$ aur ground ke beech ka altitude nikal sakte hai ?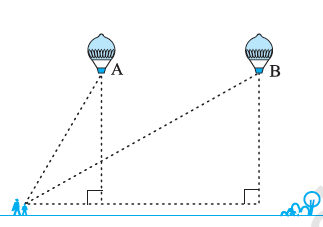

Esi tarh ki problems ko solve karne ke liye hum trigonometry ka use karte hai. ‘Trigonometry’ word derive hua hai greek words se in which ‘tri’ (meaning three), ‘gon’ (meaning sides) and ‘metron’ (meaning measure). In fact, trigonometry is the study of relationships between the sides and angles of a triangle. Astronomers iska use stars aur planets ke beech ka distance find karne ke liye karte they lekin ab Engineering aur physical sciences mein bahut se technologically advanced methods trigonometric concepts pe based hai.
Hum es chapter mein padhne vale hai about Trigonometric ratios of an acute angle of a right-angled triangle. Proof of their existence (well defined). Values of the trigonometric ratios of ${30}^{\circ }$, ${45}^{\circ }$ and ${60}^{\circ }$. Relationships between the ratios, proof and applications of some simple trigonometric identities.

To bachcho jaisa ki triangles chapter mein apne sides ke ratio ke baare mein padha hai vse hi abhi hum ek right angle triangle ki sides ke ratios nikalenge. To chalo ek example consider karte hai,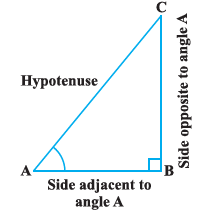

To maan lo humne ye right angle triangle ABC ko consider kiya as shown in figure above.
To dekho yha $\angle CAB$ (or angle $A$) ek acute angle hai aur side $BC$ ka position note karo w.r.t. $\angle A$. It faces $\angle A$. We call it the side opposite to $\angle A$. Aur jaisa ki hum dekh saktey hai ki $BC$ perpendicular, $AC$ hypotenuse aur $AB$ base(side adjacent to $\angle A$) of right angle triangle hai. Humey ye yaad rakhna hai ki agar hum $\angle C$ ko $\angle A$ ki jagh consider kartey ha to sides ka position change ho jayega.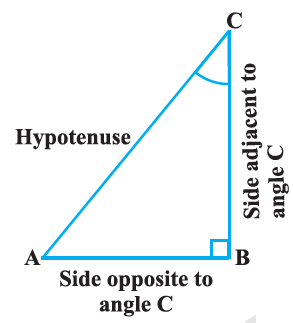

Ab hum kuch aise ratios ko define karenge jisme sides of a right triangle involved hongi. You can see that es triangle mein $3$ sides hai $AB,BC$ and $AC$ aur agar hum inke ratio nikale to hume $6$ ratios milenge, $\frac{BC}{AC}$ ,$\frac{AB}{AC}$ ,$\frac{BC}{AB}$ ,$\frac{AC}{BC}$ ,$\frac{AC}{AB}$ ,$\frac{AB}{BC}$. Inhi ratios ko hum trigonometric ratios bolte hai.
The trigonometric ratios of the $\angle A$ in right triangle $ABC$ are defined as follows:
1. sine of $\angle A$
$=\frac{\text{side opposite to angle A}}{\text{Hypotenuse}}$
$=\frac{\text{Perpendicular}}{\text{Hypotenuse}}$
$=\frac{BC}{AC}$
2. cosine of $\angle A$
$=\frac{\text{side adjacent to angle A}}{\text{Hypotenuse}}$
$=\frac{\text{Base}}{\text{Hypotenuse}}$
$=\frac{AB}{AC}$
3. tangent of $\angle A$
$=\frac{\text{side opposite to angle A}}{\text{side adjacent to angle A}}$
$=\frac{\text{Perpendicular}}{\text{Base}}$
$=\frac{BC}{AB}$
4. cosecant of $\angle A$
$=\frac{1}{\text{sine of}\angle A}$
$=\frac{\text{Hypotenuse}}{\text{side opposite to angle A}}$
$=\frac{\text{Hypotenuse}}{\text{Perpendicular}}$
$=\frac{AC}{BC}$
5. secant of $\angle A$
$=\frac{1}{\text{cosine of}\angle A}$
= $\frac{\text{Hypotenuse}}{\text{side adjacent to angle A}}$
$=\frac{\text{Hypotenuse}}{\text{Base}}$
$=\frac{AC}{AB}$
6. cotangent of $\angle A$
$=\frac{1}{\text{tangent of}\angle A}$
$=\frac{\text{side adjacent to angle A}}{\text{side opposite to angle A}}$
$=\frac{\text{Base}}{\text{Perpendicular}}$
$=\frac{AB}{BC}$
In ratios ko short mei hum $\text{sin}A$, $\text{cos}A$, $\text{tan}A$, $\text{cosec}A$, $\text{sec}A$ and $\text{cot}A$ kahte hai. And $\text{cosec}A,\text{sec}A$, aur $\text{cot}A$ reciprocals hai $\text{sin}A,\text{cos}A$, aur $\text{tan}A$ ke respectively.
$\tan A$ = $\frac{\sin A}{\cos A}$ and $\cot A$ = $\frac{\cos A}{\sin A}$
So the trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Note : The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains the same.

In a $\Delta ABC$ right-angled at B, if AB = 4, BC = 3, find all the six trigonometric ratios of $\angle A$.

We have, $AB=4$ and $BC=3$.
Ab hum yha per Pythagoras theorem ko apply karte hai to, we have
$A{C}^2=A{B}^2+B{C}^2$
$\Rightarrow AC=\sqrt{A{B}^2+B{C}^2}$
$\Rightarrow AC=\sqrt{4^2+3^2}=\sqrt{25}=5$

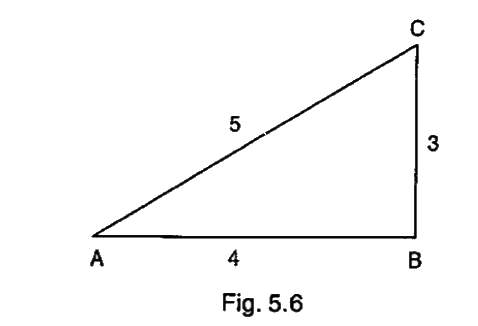
When we consider the t-ratios of $\angle A$, we have
Base = adjacent side to $\angle A=AB=4$, Perpendicular = opposite side to $\angle A=BC=3$ and Hypotenuse $=AC=5$.
$\therefore$ $\sin A=\frac{BC}{AC}=\frac{3}{5}$,
$\cos A=\frac{AB}{AC}=\frac{4}{5}$,
$\tan A=\frac{BC}{AB}=\frac{3}{4}$,
$\text{cosec}A=\frac{AC}{BC}=\frac{5}{3}$,
$\sec A=\frac{AC}{AB}=\frac{5}{4}$,
and $\cot A=\frac{AB}{BC}=\frac{4}{3}$

In $\Delta PQR$, right - angled at $Q$, $PR+QR=25\text{cm}$ and $PQ=5\text{cm}$. Determine the values of $\sin P$, $\cos P$ and $\tan P$.

It is given that $△PQR$ is right angled at $Q$.
Let's say $QR$ is the side opposite to angle $P$ and $PQ$ adjacent to angle $P$.
And $PR+QR=25\text{cm}$
So, $PR=(25-QR)\text{cm}...\left(i\right)$
In $△PQR$, by Pythagoras theorem, we have
$P{R}^2=Q{R}^2+P{Q}^2$
$\Rightarrow {(25-QR)}^2=Q{R}^2+5^2$ (From eq. $\left(i\right)$)
$\Rightarrow 625+Q{R}^2-50QR=Q{R}^2+25$
(By using ${(a-b)}^2=a^2+b^2-2ab$)
$\Rightarrow 50QR=625-25=600$
$\Rightarrow QR=12\text{cm}$
Therefore, from (i) $PR=(25-12)\text{cm}=13\text{cm}$
Now, $\sin P=\frac{QR}{PR}=\frac{12}{13}$
$\cos P=\frac{PQ}{PR}=\frac{5}{13}$
and $\tan P=\frac{QR}{PQ}=\frac{12}{5}$

To bachcho geometry se aap sab already familiar hai so you also know the construction of angles of $0^{\circ }$, ${30}^{\circ }$, ${45}^{\circ }$, ${60}^{\circ }$ and ${90}^{\circ }$. To ab hum inhi angles ki trigonometric ratios ko find out karenge.
Trigonometric Ratios of ${45}^{\circ }$
In $△ABC$, right-angled at $B$, if one angle is ${45}^{\circ }$, then the other angle is also ${45}^{\circ }$, i.e., $\angle A=\angle C={45}^{\circ }$

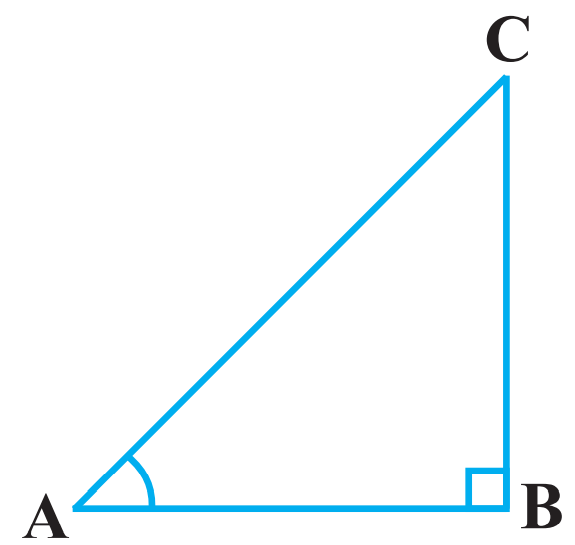
Since we know that, in triangle sides opposite to equal angle are equal, So $BC=AB.$
Suppose $BC=AB=a$
Now, by Pythagoras Theorem, $A{C}^2=A{B}^2+B{C}^2$
$=a^2+a^2=2a^2$
$AC=a\sqrt{2}$
Using the definitions of the trigonometric ratios, we have :
${\sin 45}^{\circ }=\frac{\text{side opposite to angle}{45}^{\circ }}{\text{hypotenuse}}$$=\frac{BC}{AC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$
${\cos 45}^{\circ }=\frac{\text{side adjacent to angle}{45}^{\circ }}{\text{hypotenuse}}$$=\frac{AB}{AC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$
${\tan 45}^{\circ }=\frac{\text{side opposite to angle}{45}^{\circ }}{\text{side adjacent to angle}{45}^{\circ }}$$=\frac{BC}{AB}=\frac{a}{a}=1$
$\text{cosec}{45}^{\circ }=\frac{1}{{\sin 45}^{\circ }}=\sqrt{2}$, ${\sec 45}^{\circ }=\frac{1}{{\cos 45}^{\circ }}=\sqrt{2}$, ${\cot 45}^{\circ }=\frac{1}{{\tan 45}^{\circ }}=1$

Trigonometric Ratios of ${30}^{\circ }$ and ${60}^{\circ }$
Consider an equilateral triangle $ABC$. Since each angle in an equilateral triangle is ${60}^{\circ }$, therefore, $\angle A=\angle B=\angle C={60}^{\circ }$. Draw the perpendicular $AD$ from $A$ to the side $BC$

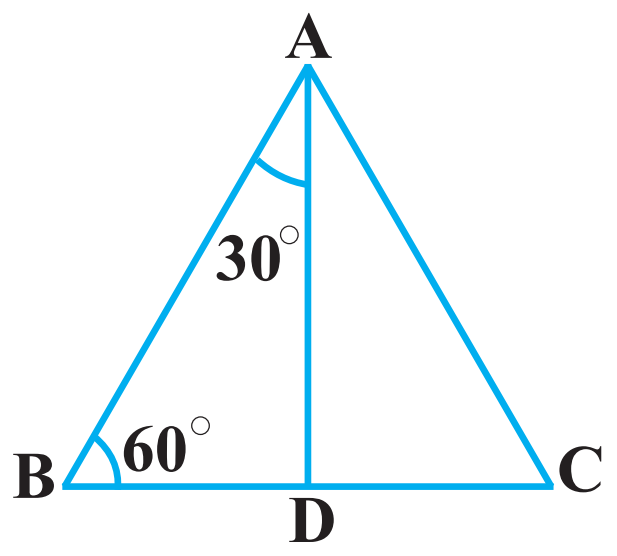
Now in $△ABD$ and $△ACD$
$AD=AD$ [common]
$\angle ADB=\angle ADC={90}^{\circ }$
$AB=AC$ [side of equilateral $△$]
Therefore, $\Delta ABD\cong \Delta ACD$ (By RHS Congruence rule)
Therefore, $BD=DC$ and $\angle BAD=\angle CAD$ (CPCT)
So, $\angle BAD$ = $\frac{1}{2}(\angle BAC$) = ${30}^{\circ }$
Now, $△ABD$ is a right triangle, right-angled at $D$ with $\angle BAD={30}^{\circ }$ and $\angle ABD={60}^{\circ }$.
Suppose that $AB=BC=CA=2a$
Then, $BD=\frac{1}{2}\left(BC\right)=a$
and $A{D}^2=A{B}^2-B{D}^2={\left(2a\right)}^2-{\left(a\right)}^2$$=3a^2$
Therefore, $AD=a\sqrt{3}$
${\sin 30}^{\circ }=\frac{BD}{AB}=\frac{a}{2a}=\frac{1}{2}$
${\cos 30}^{\circ }=\frac{AD}{AB}=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}$
${\tan 30}^{\circ }=\frac{BD}{AD}=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}}$
$\text{cosec}{30}^{\circ }=\frac{1}{{\sin 30}^{\circ }}=2$
${\sec 30}^{\circ }=\frac{1}{{\cos 30}^{\circ }}=\frac{2}{\sqrt{3}}$
${\cot 30}^{\circ }=\frac{1}{{\tan 30}^{\circ }}=\sqrt{3}$
Similarly,
${\sin 60}^{\circ }=\frac{AD}{AB}=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}$
${\cos 60}^{\circ }=\frac{1}{2}$
${\tan 60}^{\circ }=\sqrt{3}$
$\text{cosec}{60}^{\circ }=\frac{2}{\sqrt{3}}$
${\sec 60}^{\circ }=2$
${\cot 60}^{\circ }=\frac{1}{\sqrt{3}}$

Trigonometric Ratios of $0^{\circ }$ and ${90}^{\circ }$
In the right triangle $ABC$, $\angle A$ gets smaller and smaller, then length of the side $BC$ decreases to become zero and length of side $AC$ becomes almost the same as $AB$ then $\angle A$ is $0^{\circ }.$

${\sin 0}^{\circ }=\frac{BC}{AC}=\frac{BC}{AB}=0$
${\cos 0}^{\circ }=\frac{AC}{AB}=\frac{AB}{AB}=1$
${\tan 0}^{\circ }=\frac{{\sin 0}^{\circ }}{{\cos 0}^{\circ }}=0$
${\cot 0}^{\circ }=\frac{1}{{\tan 0}^{\circ }}=$not defined
${\sec 0}^{\circ }=\frac{1}{{\cos 0}^{\circ }}=1$
$\text{cosec}{0}^{\circ }=\frac{1}{{\sin 0}^{\circ }}=$not defined
Again $\angle A$ gets larger and larger, then length of the side $AB$ decreases to become zero and length of side $AC$ becomes almost the same as $BC$ then $\angle A$ is ${90}^{\circ }$

${\sin 90}^{\circ }=\frac{BC}{AC}=\frac{BC}{BC}=1$
${\cos 90}^{\circ }=\frac{AB}{AC}=0$
${\tan 90}^{\circ }=\frac{{\sin 90}^{\circ }}{{\cos 90}^{\circ }}=$not defined
${\cot 90}^{\circ }=\frac{1}{{\tan 90}^{\circ }}=0$
${\sec 90}^{\circ }=\frac{1}{{\cos 90}^{\circ }}=$not defined
$\cos ec{90}^{\circ }=\frac{1}{{\sin 90}^{\circ }}=1$
Ab in sabhi trigonometric ratios ko hum tabular form mein ek sath likhte hai.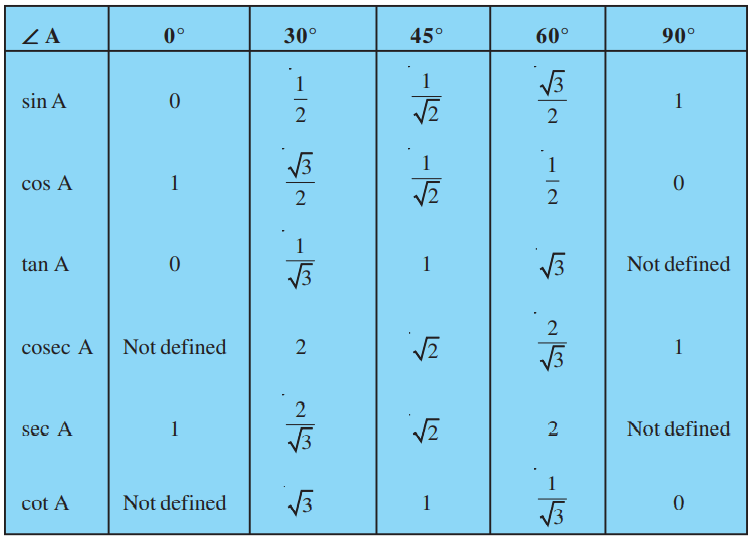

Note : $\angle A$ increases from $0^{\circ }$ to ${90}^{\circ }$, $\sin A$ increases from $0$ to $1$ and $\cos A$ decreases from $1$ to $0$. Similarly, $\tan A$ and $\sec A$ increases and $\text{cosec}A$ and $\cot A$ decreases.

Taking $\theta ={30}^{\circ }$, verify each of the following
$\left(i\right)$ $\sin 3\theta =3\sin \theta -4{\sin }^3\theta$
$\left(ii\right)$ $\cos 3\theta =4{\cos }^3\theta -3\cos \theta$

When $\theta ={30}^{\circ }$, we have $3\theta ={90}^{\circ }$.
$\left(i\right)$ $\sin 3\theta ={\sin 90}^{\circ }=1$
And, $3\sin \theta -4{\sin }^3\theta =3{\sin 30}^{\circ }-4{\sin }^3{30}^{\circ }$
$[3\times \frac{1}{2}-4\times {\left(\frac{1}{2}\right)}^3]=(\frac{3}{2}-4\times \frac{1}{8})$
$=(\frac{3}{2}-\frac{1}{2})=1$.
$\therefore \sin 3\theta =3\sin \theta -4{\sin }^3\theta$.
$\left(ii\right)$ $\cos 3\theta ={\cos 90}^{\circ }=0$.
And, $4{\cos }^3\theta -3\cos \theta =4{\cos }^3{30}^{\circ }-3{\cos 30}^{\circ }$
$=[4\times {\left(\frac{\sqrt{3}}{2}\right)}^3-3\times \frac{\sqrt{3}}{2}]$
$=(4\times \frac{3\sqrt{3}}{8}-\frac{3\sqrt{3}}{2})$
$=(\frac{3\sqrt{3}}{2}-\frac{3\sqrt{3}}{2})=0$.
$\therefore \cos 3\theta =4{\cos }^3\theta -3\cos \theta$.

If $\sin (A-B)=\frac{1}{2},\cos (A+B)=\frac{1}{2},$
$0^{\circ }<(A+B)\le {90}^{\circ }$, $A>B$, find A and B.

Since, $\sin (A-B)=\frac{1}{2}$
therefore, $A-B={30}^{\circ }$ $\to \left(1\right)$
(because $\sin$ ki value $\frac{1}{2}$ kab hoti hai ${\sin 30}^{\circ }$ pe to agar hum compare kare to $A-B={30}^{\circ }$)
Also, $\cos (A+B)=\frac{1}{2}$, therefore, $A+B={60}^{\circ }$ $\to \left(2\right)$
(because $\cos$ ki value $\frac{1}{2}$ kab hoti hai ${\cos 60}^{\circ }$ pe to agar hum compare kare to $A-B={60}^{\circ }$)
Solving $\left(1\right)$ and $\left(2\right)$, we get : $A={45}^{\circ }$ and $B={15}^{\circ }$

If $\tan (A+B)=\sqrt{3}$ and $\tan (A-B)=\frac{1}{\sqrt{3}};$$0^{\circ }\le A+B\le {90}^{\circ }$ and $A\le B,$find A and B.

Here, $\tan (A+B)=\sqrt{3}={\tan 60}^{\circ }$
So, $A+B={60}^{\circ }\to \left(1\right)$
$\tan (A-B)=\frac{1}{\sqrt{3}}={\tan 30}^{\circ }$
So, $A-B={30}^{\circ }\to \left(2\right)$
Adding $\left(1\right)$ and $\left(2\right)$,
$2A=90$
$\Rightarrow A={45}^{\circ }$
Putting value of $A$ in $\left(1\right)$,
$B=60-45={15}^{\circ }$.

In $△ABC$, right-angled at $B$,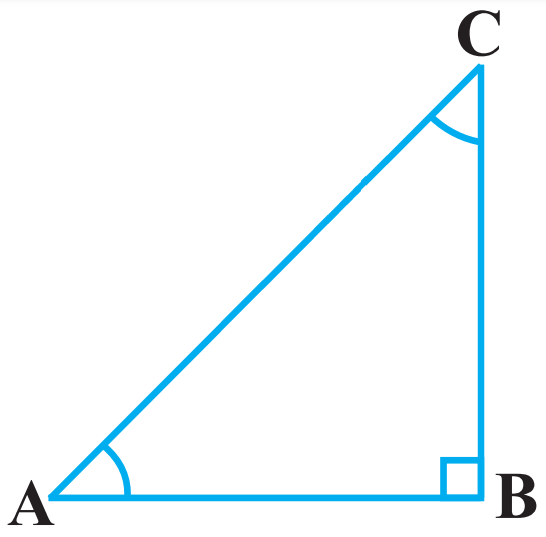

To dekho triangles ke teeno angles ka sum kya hota hai $={180}^{\circ }$
$\angle A+\angle B+\angle C={180}^{\circ }$
$\angle A+{90}^{\circ }+\angle C={180}^{\circ }$ (Since $\angle B$ is right angle)
$\angle C={90}^{\circ }-\angle A$
To ek baar hum $\angle A$ ke liye trigonometric ratios define karte hai
$\sin A=\frac{BC}{AC},$ $\cos A=\frac{AB}{AC},$ $\tan A=\frac{BC}{AB},$ $\text{cosec}A=\frac{AC}{BC},$ $\sec A=\frac{AC}{AB},$ $\cot A=\frac{AB}{BC}$
To agar hum $\angle C$ ke liye trigonometric ratios likhe to hum kya karenge $\angle A$ ko replace kar denge $\angle C$ se since ($\angle C={90}^{\circ }-\angle A$) then we get,
$\sin ({90}^{\circ }-A)=\frac{AB}{AC}=\cos A$
$\cos ({90}^{\circ }-A)=\frac{BC}{AC}=\sin A$
$\tan ({90}^{\circ }-A)=\frac{AB}{BC}=\cot A$
$\cot ({90}^{\circ }-A)=\frac{BC}{AB}=\tan A$
$\sec ({90}^{\circ }-A)=\frac{AC}{BC}=\text{cosec}A$
$\text{cosec}({90}^{\circ }-A)=\frac{AC}{AB}=\sec A$
Therefore $\sin$ and $\cos$ are complementary function to each other, $\tan$ and $\cot$ are complementary function to each other and $\text{cosec}$ and $\text{sec}$ are complementary function to each other.

Without using trigonometric tables, evaluate :
$\left(i\right)$ $\frac{{\cos 53}^{\circ }}{{\sin 37}^{\circ }}$
$\left(ii\right)$ $\frac{{\tan 68}^{\circ }}{{\cot 22}^{\circ }}$
$\left(iii\right)$ $\frac{{\sec 49}^{\circ }}{\text{cosec}{41}^{\circ }}$

$\left(i\right)$ $\frac{{\cos 53}^{\circ }}{{\sin 37}^{\circ }}=\frac{\cos ({90}^{\circ }-{37}^{\circ })}{{\sin 37}^{\circ }}=\frac{{\sin 37}^{\circ }}{{\sin 37}^{\circ }}=1$
$[\text{because}\cos ({90}^{\circ }-\theta )=\sin \theta ]$.
$\left(ii\right)$ $\frac{{\tan 68}^{\circ }}{{\cot 22}^{\circ }}=\frac{\tan ({90}^{\circ }-{22}^{\circ })}{{\cot 22}^{\circ }}=\frac{{\cot 22}^{\circ }}{{\cot 22}^{\circ }}=\frac{{\cot 22}^{\circ }}{{\cot 22}^{\circ }}=1$
$[\text{because}\tan ({90}^{\circ }-\theta )=\cot \theta ]$
$\left(iii\right)$ $\frac{{\sec 49}^{\circ }}{\text{cosec}{41}^{\circ }}=\frac{\sec ({90}^{\circ }-{41}^{\circ })}{\text{cosec}{41}^{\circ }}=\frac{\text{cosec}{41}^{\circ }}{\text{cosec}{41}^{\circ }}=1$
$[\text{because}\sec ({90}^{\circ }-\theta )=\text{cosec}\theta ]$.

Bachcho agar apko yaad ho ki, an equation is called an identity when it is true for all values of the variables involved. Jaise ki aapne algebraic identity padhi hai 9th class mein, vse hi koi bhi equation jisme kisi angle ke trigonometric ratios involve ho wo trigonometric identity kahlati hai, if it is true for all values of the angles involved.
In $△ABC$, right-angled at $B$, we have:

By Pythagoras theorem
$A{B}^2+B{C}^2=A{C}^2...\left(1\right)$
Dividing each term of $\left(1\right)$ by $A{C}^2$, we get
$\frac{A{B}^2}{A{C}^2}+\frac{B{C}^2}{A{C}^2}=\frac{A{C}^2}{A{C}^2}$
${\left(\frac{AB}{AC}\right)}^2+{\left(\frac{BC}{AC}\right)}^2={\left(\frac{AC}{AC}\right)}^2$
${\left(\cos A\right)}^2+{\left(\sin A\right)}^2=1$
${\cos }^{2}A+{\sin }^{2}A=1...\left(2\right)$
Now on dividing each term of $\left(2\right)$ by ${\cos }^{2}A$ we get
$\frac{{\cos }^{2}A}{{\cos }^{2}A}+\frac{{\sin }^{2}A}{{\cos }^{2}A}=\frac{1}{{\cos }^{2}A}$
$1+{\tan }^{2}A={\sec }^{2}A...\left(3\right)$
Now on dividing each term of $\left(2\right)$ by ${\sin }^{2}A$ we get
$\frac{{\cos }^{2}A}{{\sin }^{2}A}+\frac{{\sin }^{2}A}{{\sin }^{2}A}=\frac{1}{{\sin }^{2}A}$
${\cot }^{2}A+1={\text{cosec}}^{2}A...\left(4\right)$
Result $\left(2\right)$, $\left(3\right)$, and $\left(4\right)$ are important result we can use to simplify our identity and also used to determine the values of other trigonometric ratios in terms of known ratio.

Prove that
$\frac{\sin \theta -\cos \theta +1}{\sin \theta +\cos \theta -1}=\frac{1}{(\sec \theta -\tan \theta )}.$

LHS $=\frac{\sin \theta -\cos \theta +1}{\sin \theta +\cos \theta -1}$
$=\frac{\frac{\sin \theta }{\cos \theta }-1+\frac{1}{\cos \theta }}{\frac{\sin \theta }{\cos \theta }+1-\frac{1}{\cos \theta }}$
[ on dividing num. and denom. by $\cos \theta$ ]
$=\frac{\tan \theta -1+\sec \theta }{\tan \theta +1-\sec \theta }=\frac{(\sec \theta +\tan \theta -1)}{(\tan \theta -\sec \theta +1)}$
$=\frac{(\sec \theta +\tan \theta )-({\sec }^2\theta -{\tan }^2\theta )}{(\tan \theta -\sec \theta +1)}\left[\text{because}(1={\sec }^2\theta -{\tan }^2\theta )\right]$
$=\frac{(\sec \theta +\tan \theta )[1-(\sec \theta -\tan \theta )]}{(\tan \theta -\sec \theta +1)}$
$=\frac{(\sec \theta +\tan \theta )(\tan \theta -\sec \theta +1)}{(\tan \theta -\sec \theta +1)}=(\sec \theta +\tan \theta ).$
$RHS=\frac{1}{(\sec \theta -\tan \theta )}$
$=\frac{1}{(\sec \theta -\tan \theta )}\times \frac{(\sec \theta +\tan \theta )}{(\sec \theta +\tan \theta )}=\frac{(\sec \theta +\tan \theta )}{({\sec }^2\theta -{\tan }^2\theta )}$
$=(\sec \theta +\tan \theta )\left[\text{because}({\sec }^2\theta -{\tan }^2\theta =1)\right].$
Hence, $LHS=RHS.$

Prove that
(i) $(1-{\sin }^2\theta ){\sec }^2\theta =1$
(ii) $(1+{\tan }^2\theta ){\cos }^2\theta =1$
(iii) $(1+{\tan }^2\theta )(1-\sin \theta )(1+\sin \theta )=1$
(iv) $2{\cos }^2\theta +\frac{2}{(1+{\cot }^2\theta )}=1$

We have
(i) LHS = $(1-{\sin }^2\theta ){\sec }^2\theta$
$={\cos }^2\theta \cdot {\sec }^2\theta$ $\left[\text{because}(1-{\sin }^2\theta ={\cos }^2\theta )\right]$
$={\cos }^2\theta \cdot \frac{1}{{\cos }^2\theta }=1=RHS.$
$\therefore$ LHS = RHS.
(ii) LHS $=(1+{\tan }^2\theta ){\cos }^2\theta$
$={\sec }^2\theta \cdot {\cos }^2\theta$ $\left[\text{because}(1+{\tan }^2\theta ={\sec }^2\theta )\right]$
$=\frac{1}{{\cos }^2\theta }\cdot {\cos }^2\theta =1=RHS.$
$\therefore$ LHS = RHS.
(iii) LHS = $(1+{\tan }^2\theta )(1-\sin \theta )(1+\sin \theta )$
$=(1+{\tan }^2\theta )(1-{\sin }^2\theta )={\sec }^2\theta \cdot {\cos }^2\theta$
$[\text{because}(1+{\tan }^2\theta )={\sec }^2\theta ,(1-{\sin }^2\theta )={\cos }^2\theta ]$
$=\frac{1}{{\cos }^2\theta }\cdot {\cos }^2\theta$ $\left[\text{because}({\sec }^2\theta =\frac{1}{{\cos }^2\theta })\right]$
$=1=RHS.$
$\therefore$ LHS = RHS.
(iv) LHS = $2{\cos }^2\theta +\frac{2}{(1+{\cot }^2\theta )}$
$=2{\cos }^2\theta +\frac{2}{{\text{cosec}}^2\theta }$ $\left[\text{because}(1+{\cot }^2\theta ={\text{cosec}}^2\theta )\right]$
$=2{\cos }^2\theta +2{\sin }^2\theta$ $\left[\text{because}(\frac{1}{{\text{cosec}}^2\theta }={\sin }^2\theta )\right]$
$=2({\cos }^2\theta +{\sin }^2\theta )=2\times 1$ $\left[\text{because}({\cos }^2\theta +{\sin }^2\theta =1)\right]$
$=2=RHS.$
$\therefore$ LHS = RHS.

1. In a right triangle $ABC$, right-angled at $B$,
$\sin A=\frac{\text{side opposite to angle}A}{\text{hypotenuse}}$
$\cos A=\frac{\text{side adjacent to angle}A}{\text{hypotenuse}}$
$\tan A=\frac{\text{side opposite to angle}A}{\text{side adjacent to angle}A}$
2. $\cos ecA=\frac{1}{\sin A};$$\sec A=\frac{1}{\cos A};$$\tan A=\frac{1}{\cot A},$$\tan A=\frac{\sin A}{\cos A}$
3. The value of $\sin A$ or $\cos A$ never exceeds $1$, whereas the value of $\sec A$ or $\cos ecA$ is always greater than or equal to $1$.
4. $\sin ({90}^{\circ }-A)=\cos A$
$\cos ({90}^{\circ }-A)=\sin A$
$\tan ({90}^{\circ }-A)=\cot A$
$\cot ({90}^{\circ }-A)=\tan A$
$\sec ({90}^{\circ }-A)=\cos ecA$
$\cos ec({90}^{\circ }-A)=\sec A$
5. ${\cos }^{2}A+{\sin }^{2}A=1$
$1+{\tan }^{2}A={\sec }^{2}A$
${\cot }^{2}A+1=\cos e{c}^{2}A$

• Trigonometry is the study of relationships between the sides and angles of a triangle.

• Trigonometric Ratios of the Angle:
  Ratios of the sides of a right triangle with respect to its acute angles.
  Suppose karo ki humarey paas ek right angle triangle hai $ABC$, right angle at $B$, aur $\angle CAB$ acute angle hai.
  $AB$ adjacent side (Base) aur $BC$ opposite side (Perpendicular) hai, $\angle A$ ke liye. To hume trigonometric ratios kuch es tarh se milte hai,
  (i) sine of $\angle A$ or sin $A=\frac{\text{perpendicular}}{\text{hypotenuse}}=\frac{BC}{AC}$
  (ii) cosine of $\angle A$ or cos A = $\frac{\text{base}}{\text{hypotenuse}}$ = $\frac{AB}{AC}$
  (iii) tangent of $\angle A$ or tan A = $\frac{\text{perpendicular}}{\text{base}}$ =$\frac{BC}{AB}$
  (iv) cosecant of $\angle A$ or cosec A = $\frac{1}{\text{sine of angleA}}$ = $\frac{\text{hypotenuse}}{\text{perpendicular}}$ = $\frac{AC}{BC}$
  (v) secant of $\angle A$ or sec A = $\frac{1}{\text{cosec of angle A}}$ = $\frac{\text{hypotenuse}}{\text{base}}$ = $\frac{AC}{AB}$
  (vi) cotangent of $\angle A$ or cot A = $\frac{1}{\text{tangent of angleA}}$ = $\frac{\text{base}}{\text{perpendicular}}$ = $\frac{AB}{BC}$
  Similarly, hum $\angle C$ ke liye bhi trigonometric ratios nikal saktey hai lekin angle $C$ ke liye perpendicular $AB$ hoga aur base $BC$ hoga.

• The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains the same.

• Trigonometric Ratios of Some Specific Angles:
  
  
  The value of sin $\theta$ and cos $\theta$ can never exceed $1$. Adjacent side can never be greater than hypotenuse since hypotenuse is the longest side in a right-angled ∆.

• Trigonometric Ratios for Complementary Angles:
  If $\Delta ABC$ is a right-angled triangle, right-angled at B, then $\angle A+\angle C=90°$ [∵ $\angle A+\angle B+\angle C=180°$ angle-sum-property] or $\angle C=(90°–\angle A).$ Yha $\angle A$ aur $\angle C$ complementary angles hai aur in relationships ko satisfy kartey hai,
  (1) sin C = sin (90° - A) = cos A
  (ii) cosec C = cosec (90° – A) = sec A
  (iii) cos C = cos (90° – A) = sin A
  (iv) sec C = sec (90° – A) = cosec A
  (v) tan C = tan (90° – A) = cot A
  (vi) cot C = cot (90° – A) = tan A

• Trigonometric Identities:
  An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved. These are
  $\tan \theta =\frac{\sin \theta }{\cos \theta }$
  $\cot \theta =\frac{\cos \theta }{\sin \theta }$
  (i) ${\cos }^{2}A+{\sin }^{2}A$ = 1
  (ii) $1+{\tan }^{2}A={\sec }^{2}A$ (for 0° ≤ A < 90°)
  (iii) ${\cot }^{2}A+1={\text{cosec}}^{2}A$ (for 0° < A ≤ 90º)