If both the roots of the quadratic equation are less than 5 , then k lies in the interval
A
B
C
D
Video Solution
Text Solution
The correct Answer is:A
Let then
Consider the following cases:
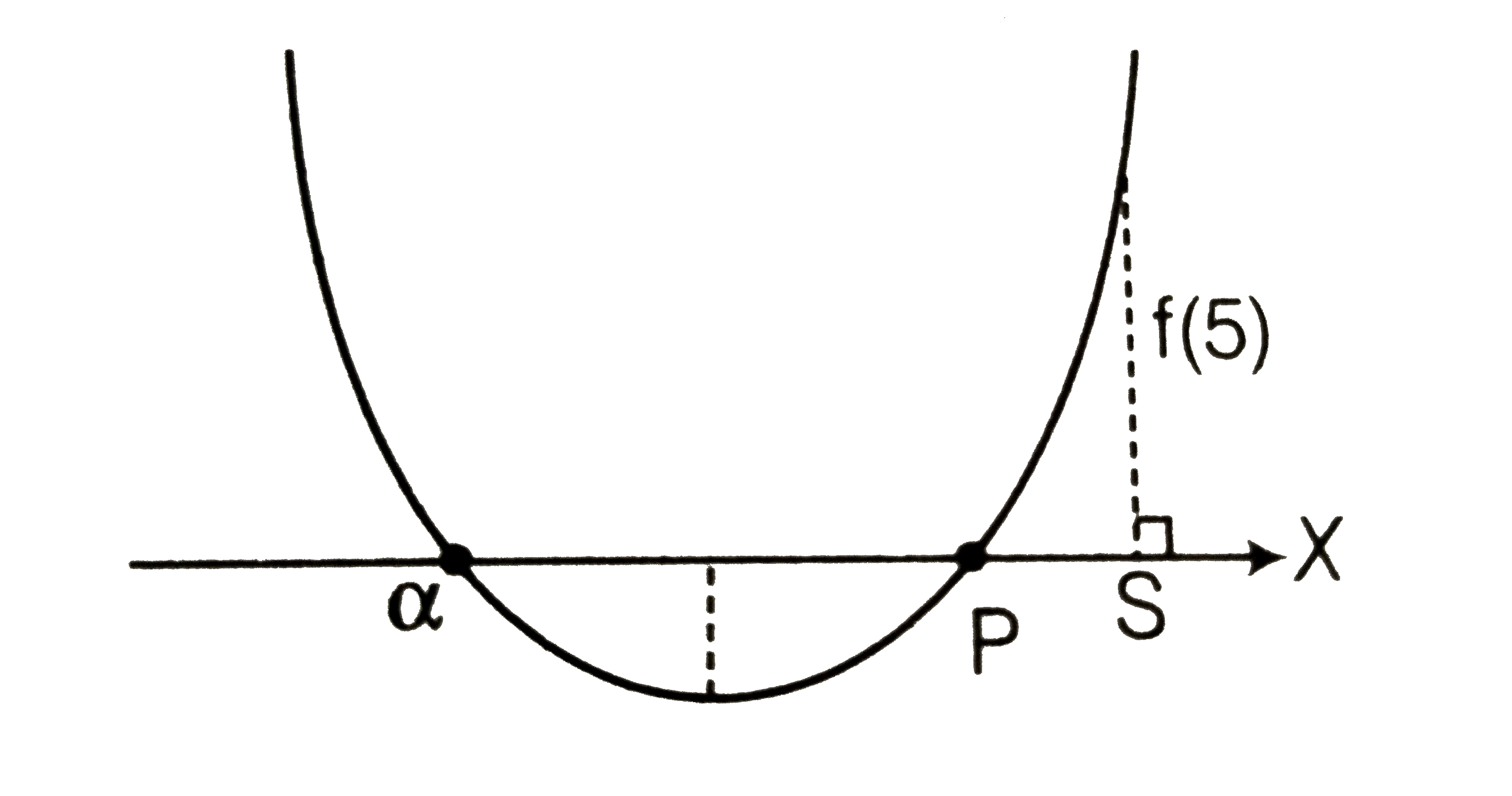
Case I
or
Case II x-Coordinate of vertex
or
Case III
or
Combining all cases, we get
|
Updated on:21/07/2023
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Subjective Type Questions)24videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Knowledge Check
- Question 1 - Select One
If both the roots of the quadratic equation x−2kx+k2−5=0 are less than 5, then k lies in the
A(−∞,4)B[4,5]C(5,6)D(6,∞) - Question 1 - Select One
If both the roots of the equation x2−12kx+k2+k−5=0 are less than 5, then k lies in the inverval
A(−∞,4)B[4,5]C[5,6]D(6,∞) - Question 1 - Select One
If the roots of the quadratic equation x2+2x+k=0 are real, then
Ak<0Bk≤0Ck<1Dk≤1 - Question 1 - Select One
If both the roots of the quadratic equation x2−mx+4=0 are real and distinct and they lie in the interval [1,5], then m lies in the interval
A(4,5)B(−5,−4)C(5,6)D(3,4) - Question 1 - Select One
If both the roots of the quadratic equation x2−mx+4=0 are real and distinct and they lie in the interval [1, 5], then m lies in the interval
A(4, 5]B(3, 4)C(5, 6)D(−5,−4)
Similar Questions
If both the roots of the quadratic equa,tion x2−2kx+k2+k−5=0 are less than 5 then k lies i the interval (A) [4,5] (B) 9−∞,4) (C) 6,∞) (D) 95,6]
View SolutionIf both roots of the quadratic equation x2+x(4−2k)+k2−3k−1=0 are less than 3, then k lies in the interval
View SolutionFind k, if the roots of the quadratic equation kx2−4x+4=0 are equal
View SolutionFind k, if the roots of the quadratic equation kx2−4x+4=0 are equal
View SolutionIf the roots of the quadratic equation x2−2kx+2k2−4=0 are real,then the range of the values of k is
View Solution

