A capacitor of capacitance $C$ is charged to a potential differece $V_{0}$ . The terminals of the charged capacitor are then connected to those of an uncharged capacitor of capacitance $C / 2$ .
a. Compute the original charge of the system.
b. Find the final potential differce across each capacitor.
c. Find the final energy of the system.
d. Calculate the decrease in energy when the capacitors are connected.
e. Where did the ''lost'' energy go?

Video Solution

Text Solution

Verified by Experts

$Q = C V_{0}$
They have equal potential difference, and thir combined charge must add up to the original charge Therefore,
$V = \frac{Q_{1}}{C_{1}} = \frac{Q_{2}}{C_{2}}$ and also $Q_{1} + Q_{2} = C V_{0}$
$C_{1} = C$ and $C_{2} = \frac{C}{2}$ ,
So $\frac{Q_{1}}{C} = \frac{Q_{2}}{(C / 2)}$
or $Q_{2} = \frac{Q_{1}}{Q_{2}}$
or $Q = \frac{3}{2} Q_{1} or Q_{1} = \frac{2}{3} Q$
So $V = \frac{Q_{1}}{C_{1}} = \frac{2}{3} \frac{Q}{C} = \frac{2}{3} V_{0}$
c. $U = \frac{1}{2} (\frac{Q_{1}^{2}}{C_{1}} + \frac{Q_{2}^{2}}{C_{2}}) = \frac{1}{2} ⎡ ⎢ ⎢ ⎢ ⎣ \frac{{(\frac{2}{3} Q)}^{2}}{C} + \frac{2 {(\frac{1}{3} Q)}^{2}}{C} ⎤ ⎥ ⎥ ⎥ ⎦$
$= \frac{1}{2} \frac{Q_{2}}{C} = \frac{1}{2} C V_{0}^{2}$
d. The original $U$ was $U = \frac{1}{2} C V_{0}^{2}$ or $Δ U = \frac{- 1}{6} C V_{0}^{2}$ .
Thermal energy of capacitor, wires, etc., and electromagnetic radiation.

Updated on:21/07/2023

A capacitor $C_{1}$ of capacitance C is charged to a potential difference $V_{0}$ . The terminal of the charged capacitor are then connected to an uncharged capacitor $C_{2}$ of capacitance $C / 2 .$ Match the entries of Column I with the entries of Column II and choose the correct option from the codes given below.

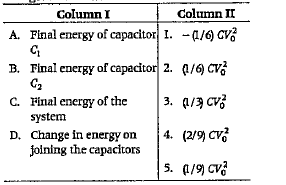A
B
C
D
A $10 μ F$ capacitor is charged to a potential difference of $1000 V$ . The terminals of the charged capacitor are disconnected from the power supply and connected to the terminals of an uncharged $6 μ F$ capacitor. What is the final potential difference across each capacitor ?
A $167 V$
B $100 V$
C $625 V$
D $250 V$
A capacitor or capacitance $C_{1}$ is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance $C_{2}$ . The fianl potential difference across each capacitor will be
A $\frac{C_{1} V}{C_{1} + C_{2}}$
B $\frac{C_{2} V}{C_{1} + C_{2}}$
C $1 + \frac{C_{2}}{C_{1}}$
D $1 - \frac{C_{2}}{C_{1}}$