In Fig.5.52, the resistances are connected as shown. Given R1=10ΩR2=20Ω. Determine the equivalent resistance between points (i) A and D and (ii) B and C

Video Solution
Text Solution
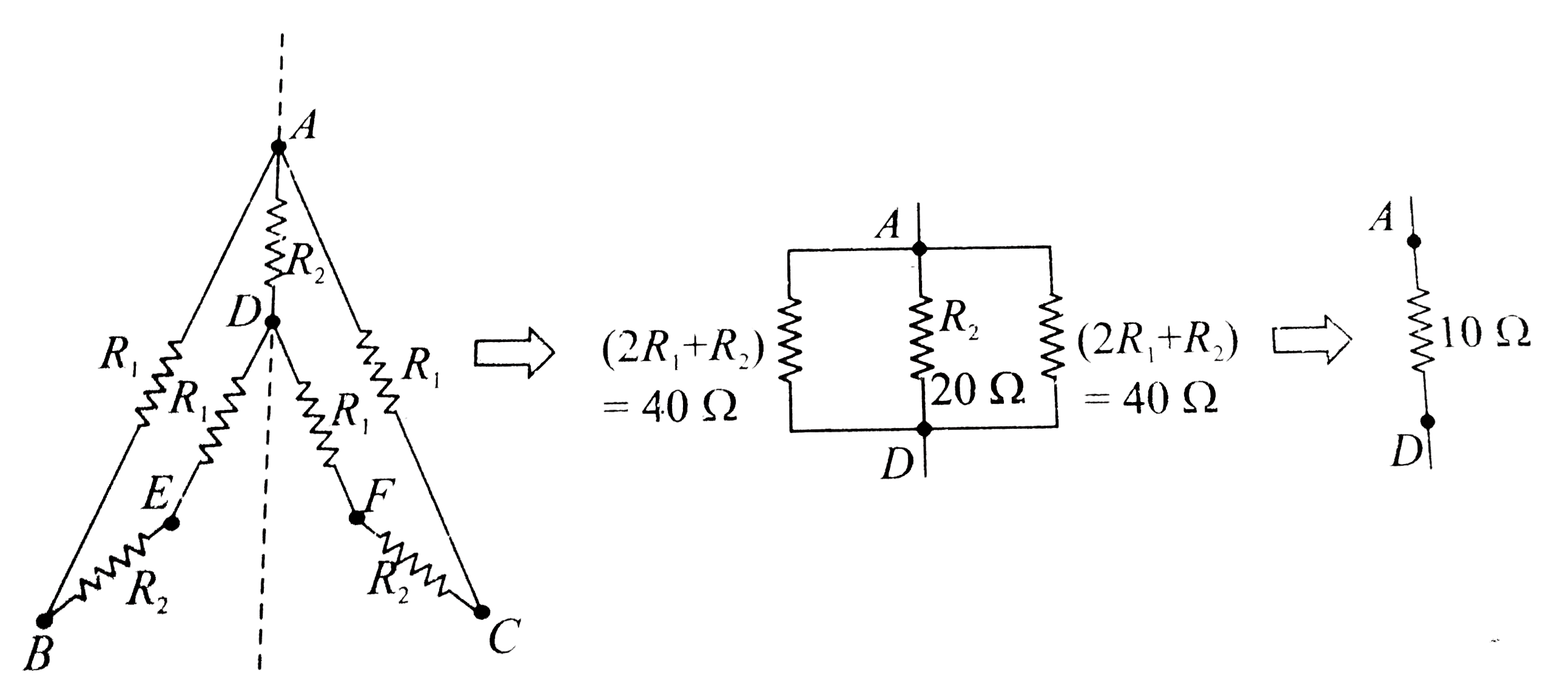
(i) Calculation of equivalent between A and D:
There exists parallel axis of symmetry. The points across the
parallel axis of symmetry can be treated as equipotntial points.
Mehod 1: Points B and C, and E and F are at the same
potential, so the circuit can be redrawn as shown in fig. 5.23.
Thus, the equivalent resistance is 10Ω
Method 2: the points with charge symmetrical to parallel axis
are equipotential points. The resistances connected between
these points can be removed. A step- by-step procedure for the
calculation of equivalent resistance is shown in Fig. 5.54
Method 3: We can fold the circuit about the parallel axis of
symmetry. The step -by - step procedure is shown in Fig. 5.55.
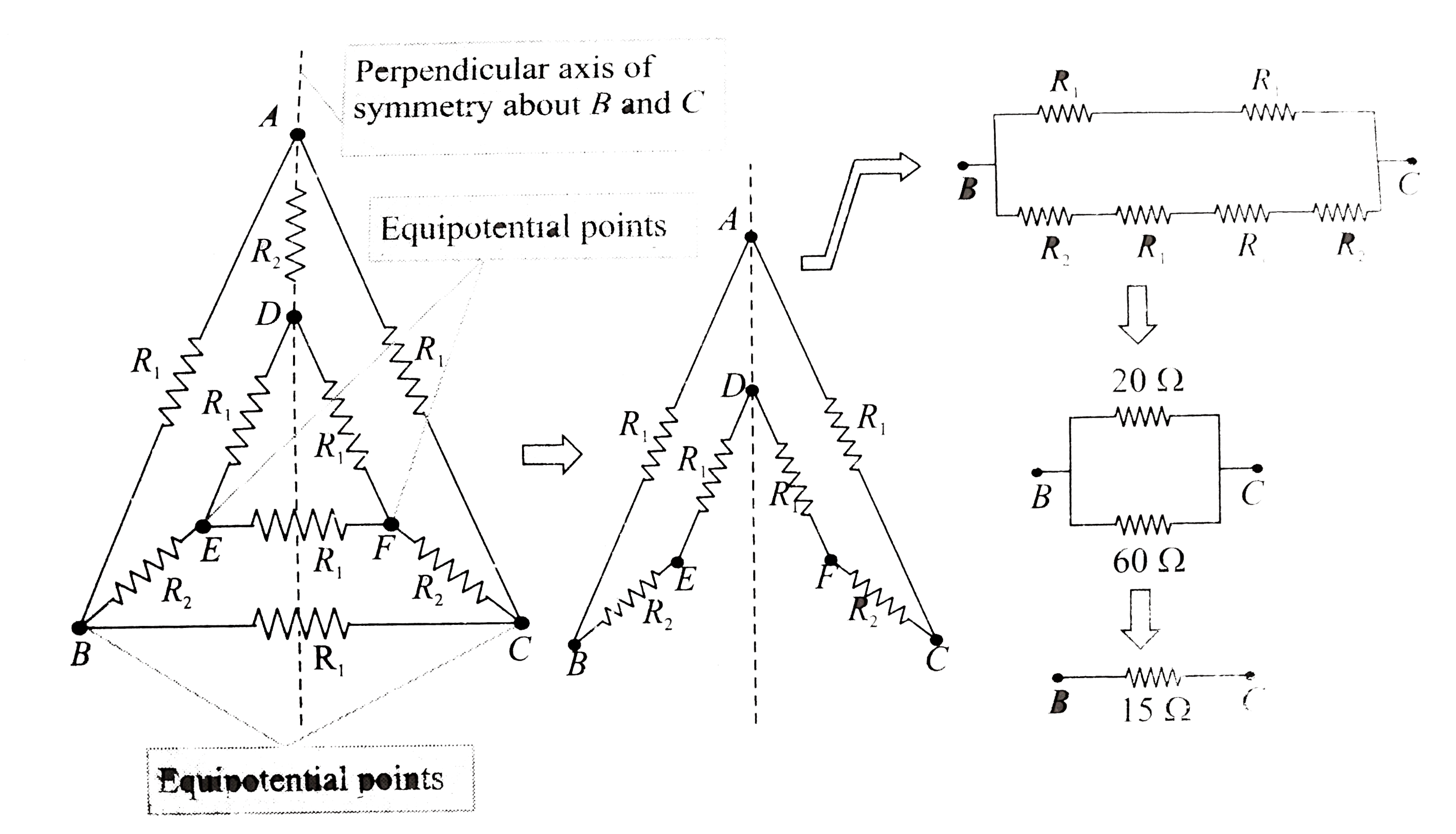
ii. Calculation of equivalent resistnace between B and C :
There exists perpendicular axis of symmetry about line x-y
Hence, the points symmetrical about x-y are equipotential,
i.e., points (E and F) and (B and C) are equipotential. Thus,
the resistance connected across these points can be removed. Also points A and D are lying on the perpendicular axis of symmetry. Hence, points A and D are also equipotential. The
resistances conneted between A and D can also be removed.
The circuit reduces as shown, and the steps - by step procedure
is given in fig. 5.56


|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Practice Problems
- Question 1 - Select One
In the given figure, R=3Ω. Determine equivalent
resistance between points A and B.
 . A3ΩB2ΩC15ΩD6Ω
. A3ΩB2ΩC15ΩD6Ω - Question 1 - Select One
Equivalent resistance between the points A and B (in Ω)
 .A15B114C213D312
.A15B114C213D312 - Question 1 - Select One
Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
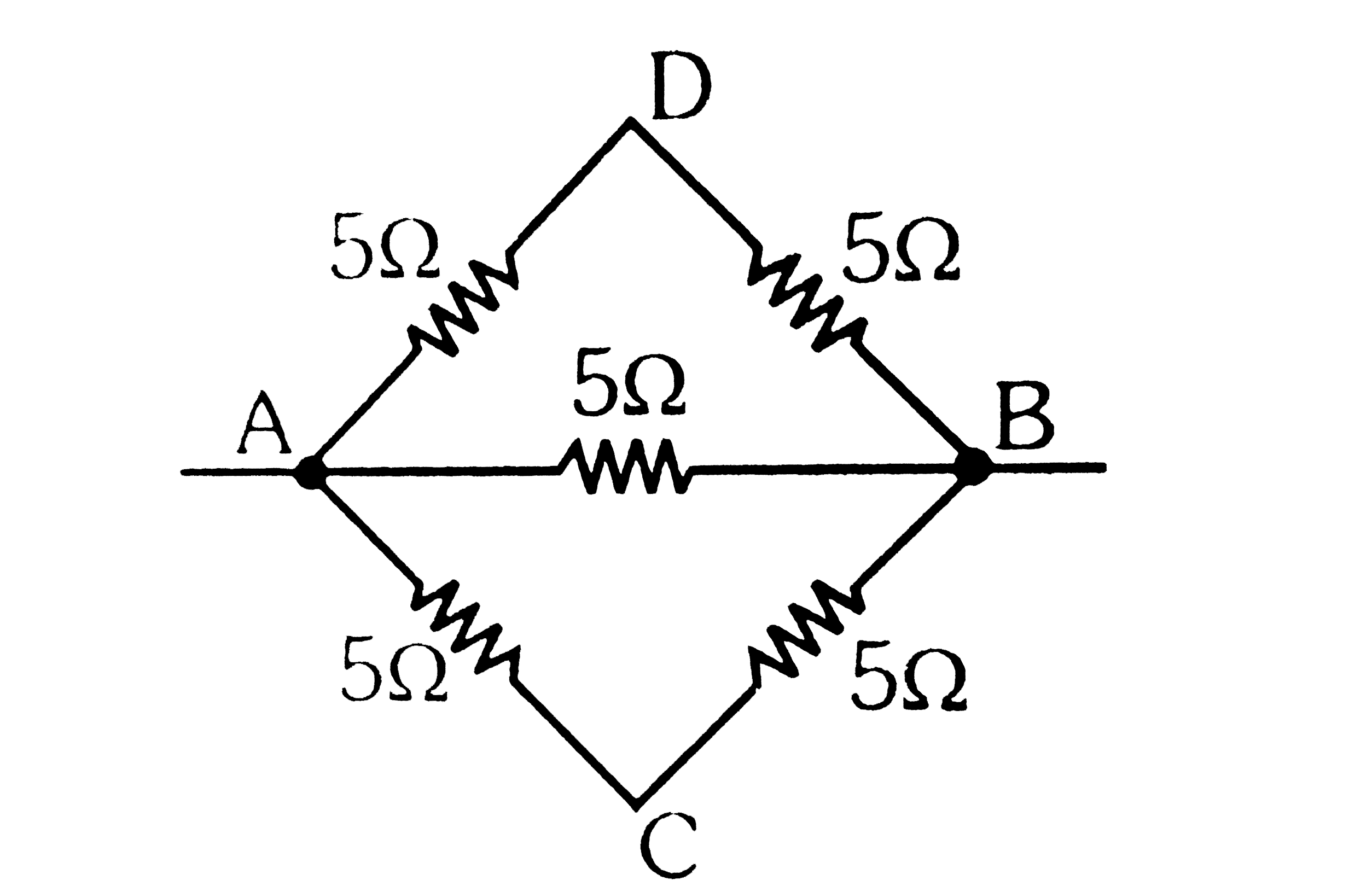 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω - Question 1 - Select One
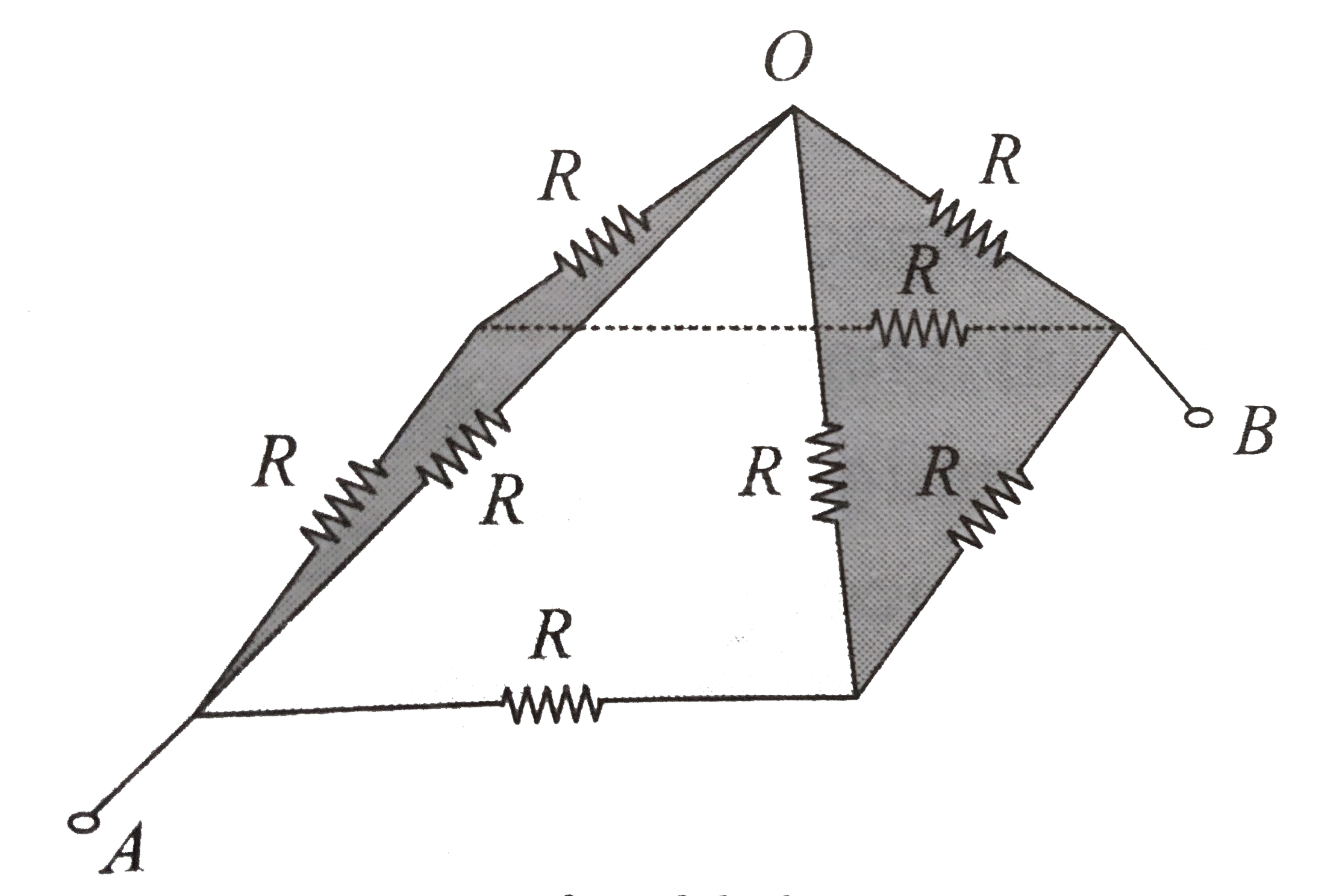
Three equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is
ArB3rCr3D2r3 - Question 1 - Select One
The equivalent resistance between points A and B in the network shown in fig. is –
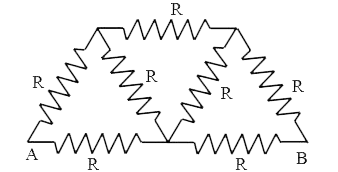 A157RB87RC127RD167R
A157RB87RC127RD167R - Question 1 - Select One
For the circuit shown in fig. the equivalent resistance between A and C is
 A1211rB1311rC1411rD1511r
A1211rB1311rC1411rD1511r - Question 1 - Select One
The equivalent resistance between the points A and B in A the circuit shown in Fig. is
 A3.12ΩB1.56ΩC6.24ΩD12.48Ω
A3.12ΩB1.56ΩC6.24ΩD12.48Ω
Similar Questions
Determine the equivalent resistance of networks shown in Fig. (i) and (ii).
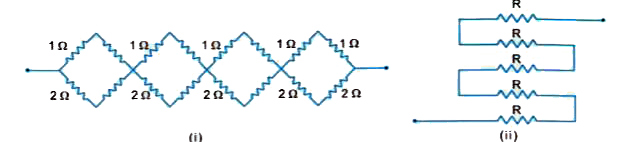 View Solution
View Solution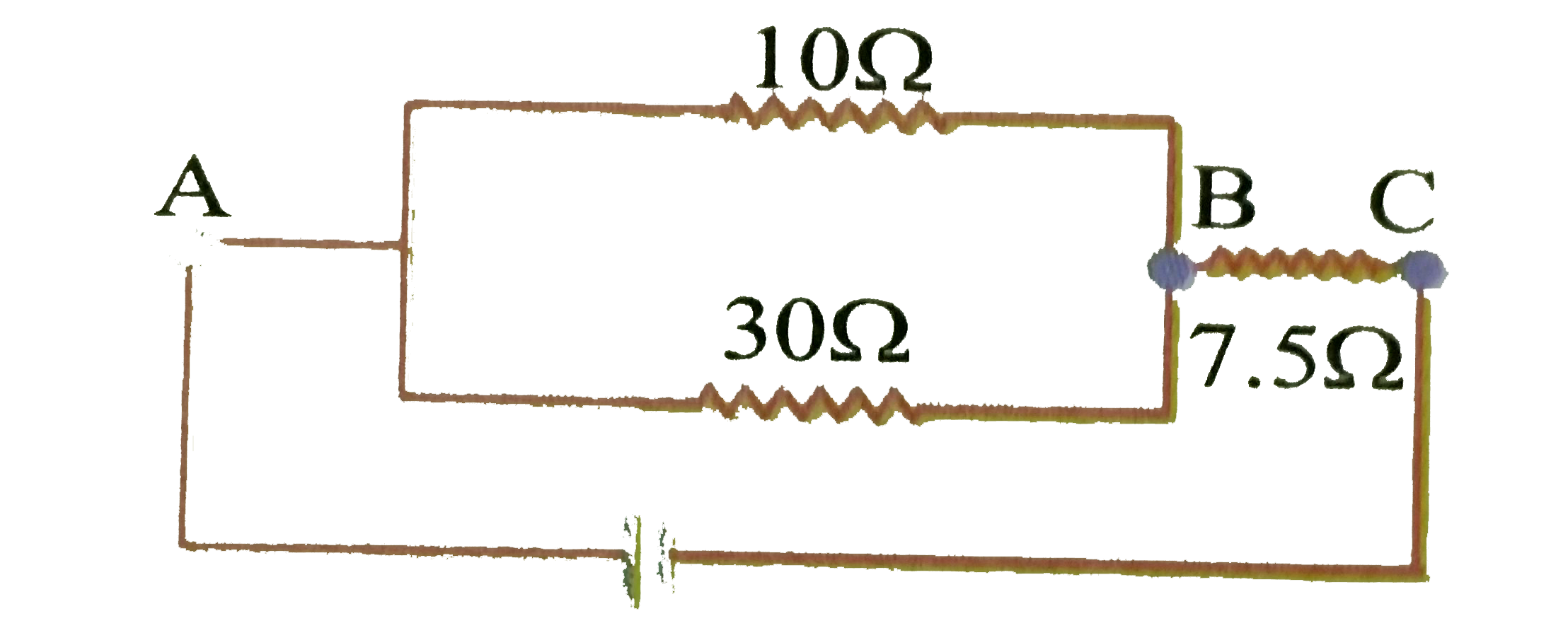
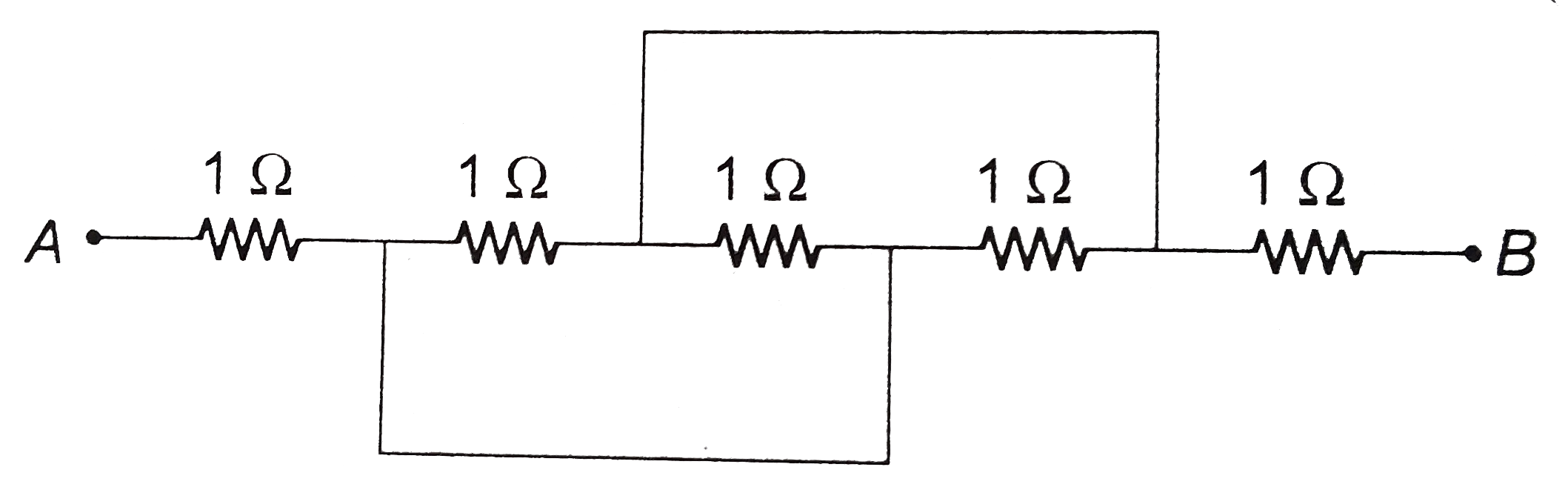
Find equivalent resistance of the network in fig. Between points (i) A and B and (ii) A and C.View SolutionIf the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
 View Solution
View Solution

