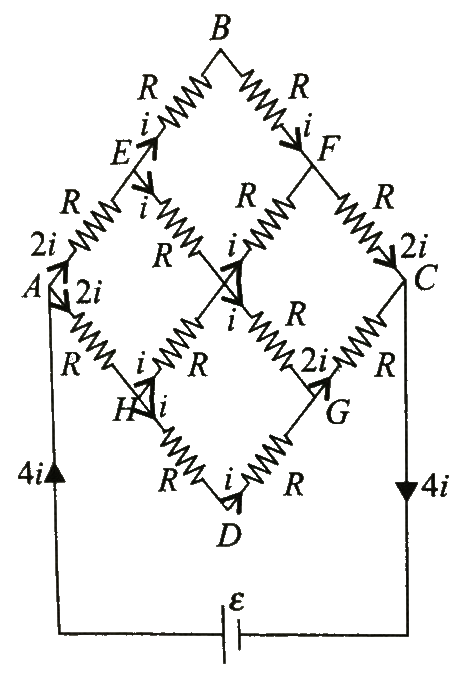
In the following network of 12 identical resistances, calculate the equivalent resistance between points A and C

Video Solution
Text Solution
An imaginary battery
of emf ε is assumed across the
terminals A and C.
Step.2 the current in each branch
is distributed by assuming 4i
current coming out of the battery.
Step 3 We apply KVL along the
outer loop including the nodes A,
B,C and the battery E. Voltage
equation is
−2iR−iR−iR−2iR+E=0
Step4 After solving the above
equation, we get 6iR=E. The
equivalent resistance between A and C is
R=E4i6iR4i=32R
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Knowledge Check
- Question 1 - Select One
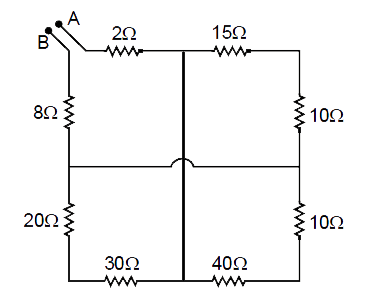
The equivalent resistance between points A and B
 A2ΩB4ΩC1ΩDNone of these
A2ΩB4ΩC1ΩDNone of these - Question 1 - Select One
The equivalent resistance between points A and B
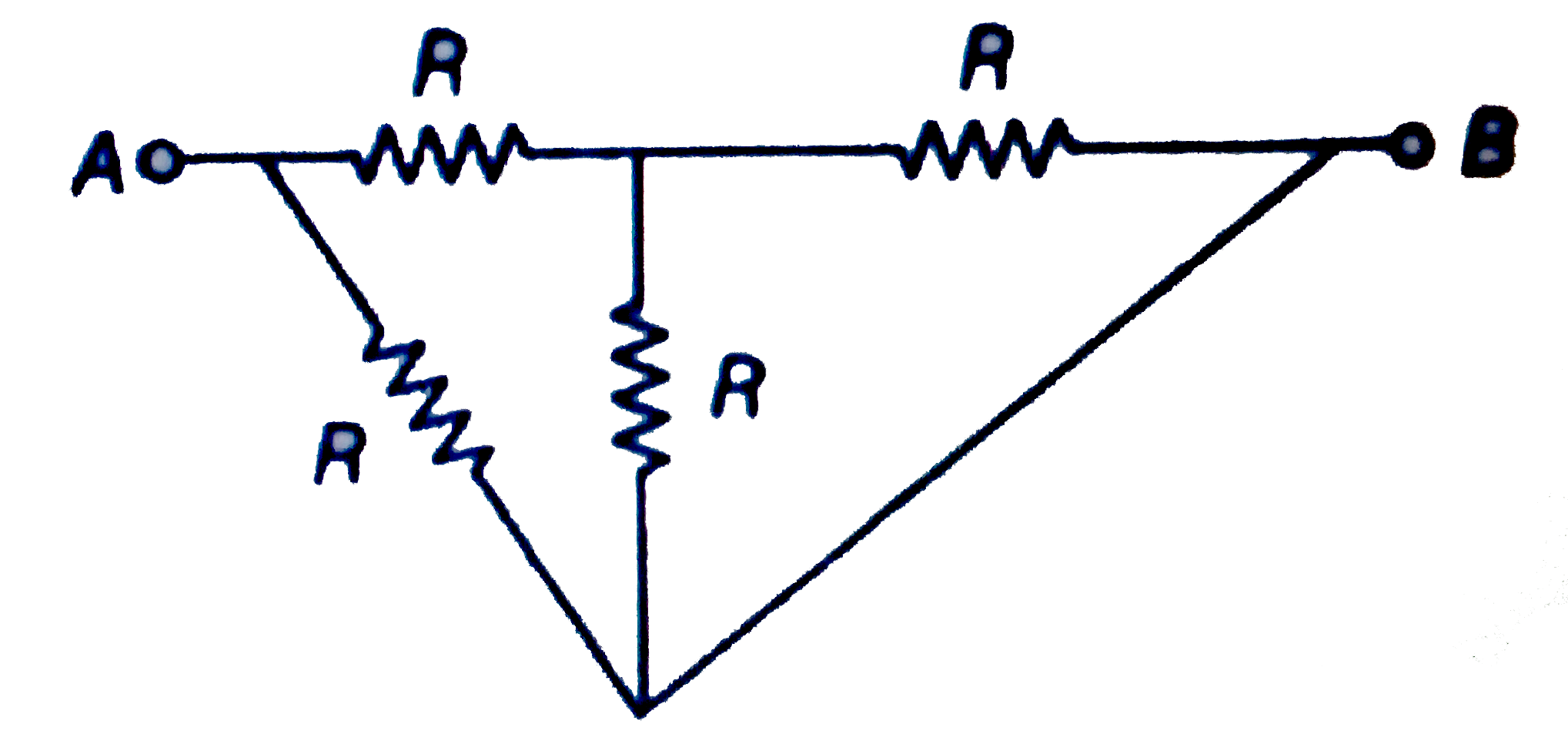 A2RB34RC43RD35R
A2RB34RC43RD35R - Question 1 - Select One
The equivalent resistance between points A and B is
 A2RB34RC43RDR
A2RB34RC43RDR - Question 1 - Select One
The equivalent resistance between points A and B is
 A32.5ΩB22.5ΩC12.5ΩD42.5Ω
A32.5ΩB22.5ΩC12.5ΩD42.5Ω - Question 1 - Select One
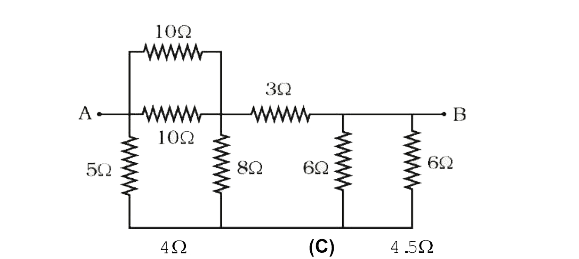
Calculate the equivalent resistance between A and B
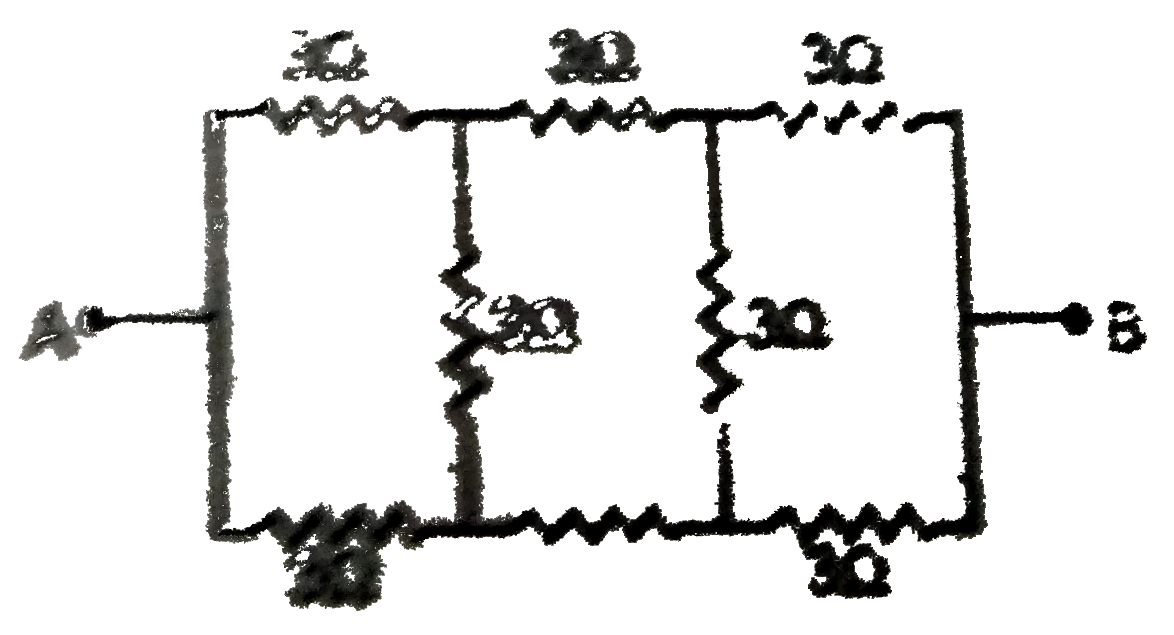 A9/2ΩB3ΩC6ΩD5/3Ω
A9/2ΩB3ΩC6ΩD5/3Ω - Question 1 - Select One
The equivalent resistance between the points A and B is:
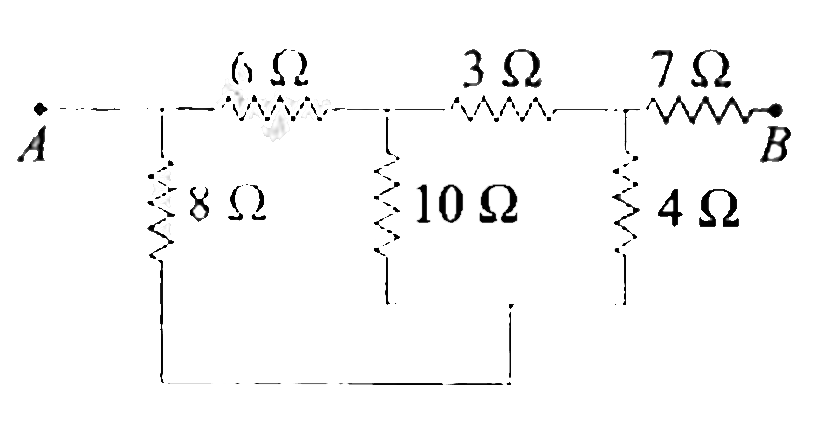 A367ΩB10ΩC857ΩDnone of these
A367ΩB10ΩC857ΩDnone of these - Question 1 - Select One
The equivalent resistance between the point A and B is
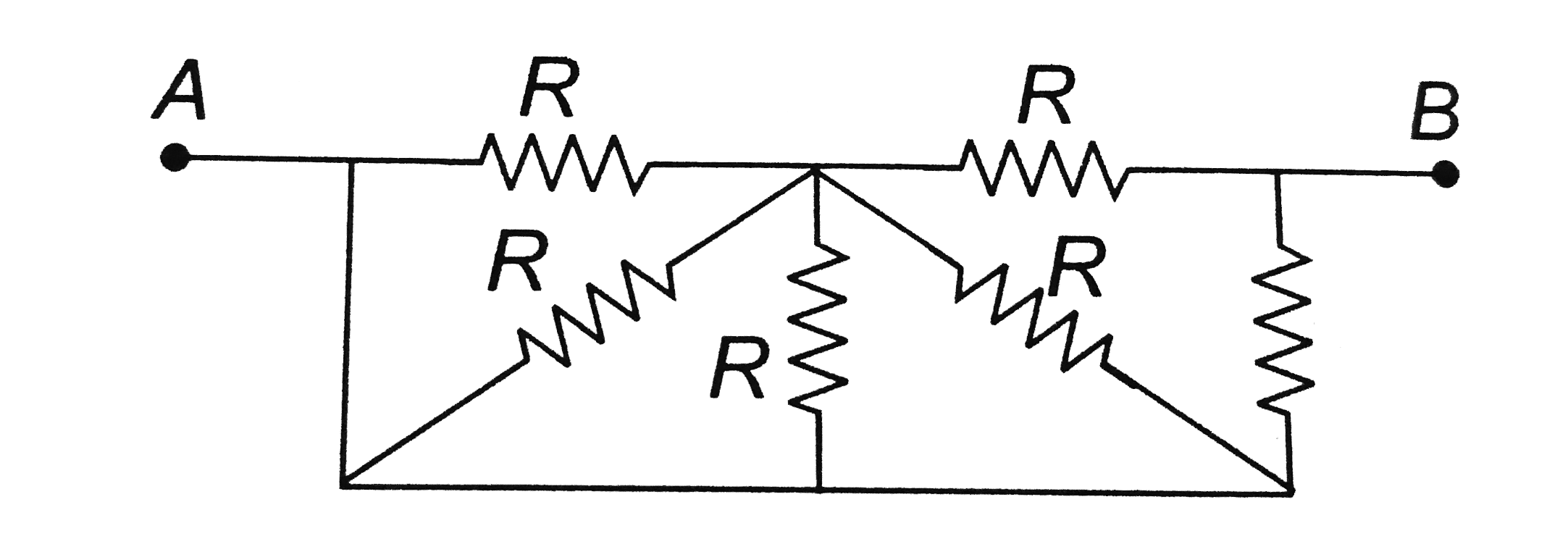 A5R9B2R3CRDNone of these
A5R9B2R3CRDNone of these - Question 1 - Select One
Calculate equivalent resistance between A and C
 A10R8B10R7C10R9D10R11
A10R8B10R7C10R9D10R11