Tweleve indentical resistor are arranged on all edfges of a cube. Then find the equivalent resistance between the corners 1 and 6 as shwon in fig 5.126(us nodal method) 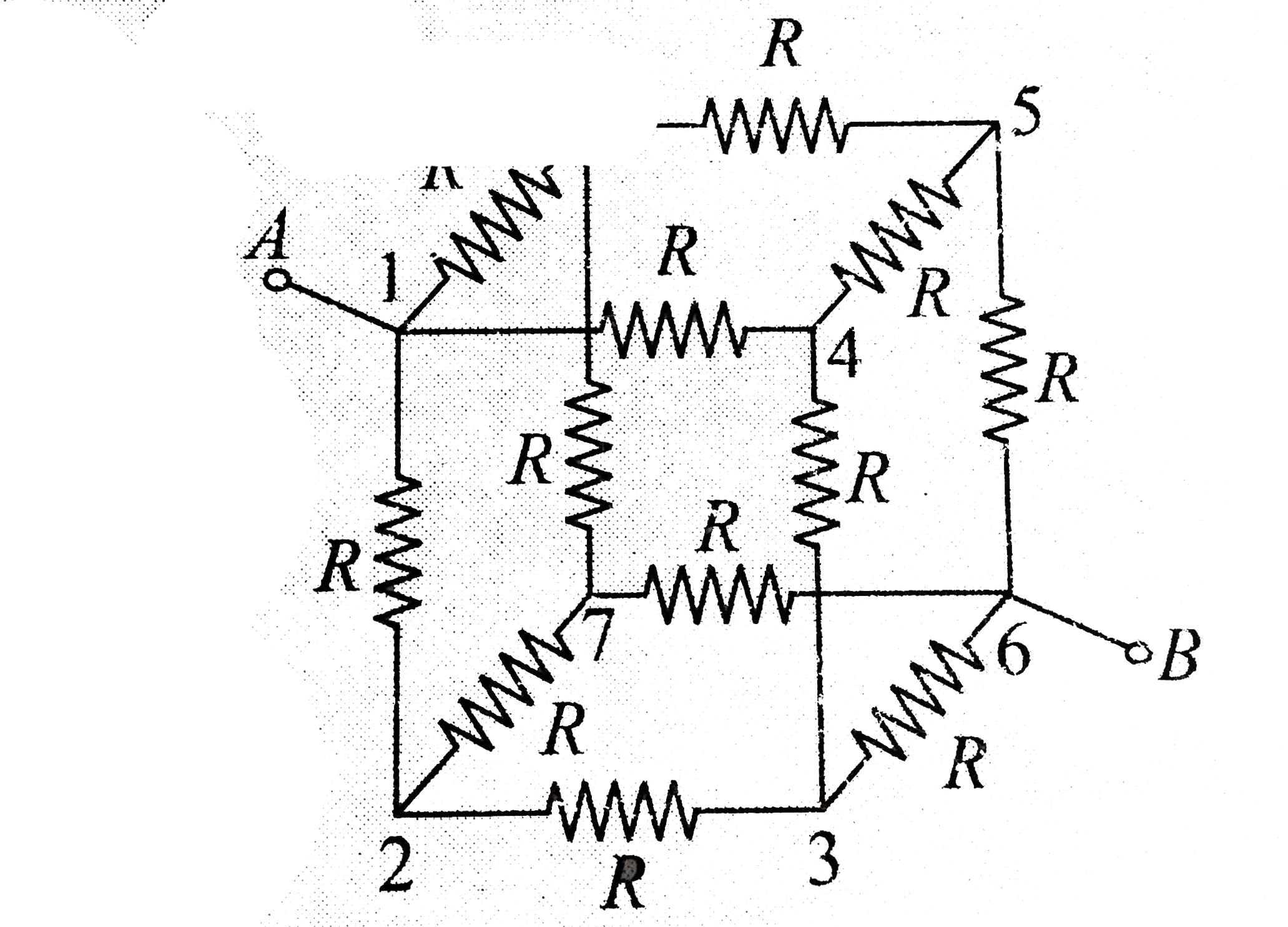
Let us assume we have
connected a battery of emf V
across points 1 and 6. if potential
of point 1 is V, then the potential
of point 6 is 0.
From symmetry, it is clear that
the current entering at point1 will equally divide the resistance. Hence, the potential differences
across resistances, conncted
across (1,8) , (1,2), and (1,4), will be equal .
Similarly the current coming out at point 6 will be equal
to current ennering at point 1. By symmetry, we can say the current in the resistances connected across points (7,6),
(3,6), and (6,5) will be equal. Hence, potential difference
across these resistance should be equal. Let us assume the
potentials at points 3,5, and 7 be x then the potentials at points 2,4, and 8 should be (V - x). At point 7,
[x−(V−x)]R+x−0R+[x−(V−x)]R=0
or x25V(i)
At point 1, I=3[V−(V−x)]R=3xR(ii)
From (i) and (ii)
VI=5R6
Hence, effective resistance will be 5R/6.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in.
 View Solution
View SolutionFind the equivalent resistance between the points A and B of the network of resistors shown in Fig. 4.16.
View Solution
Knowledge Check
- Question 1 - Select One
Each of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4 - Question 2 - Select One
Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
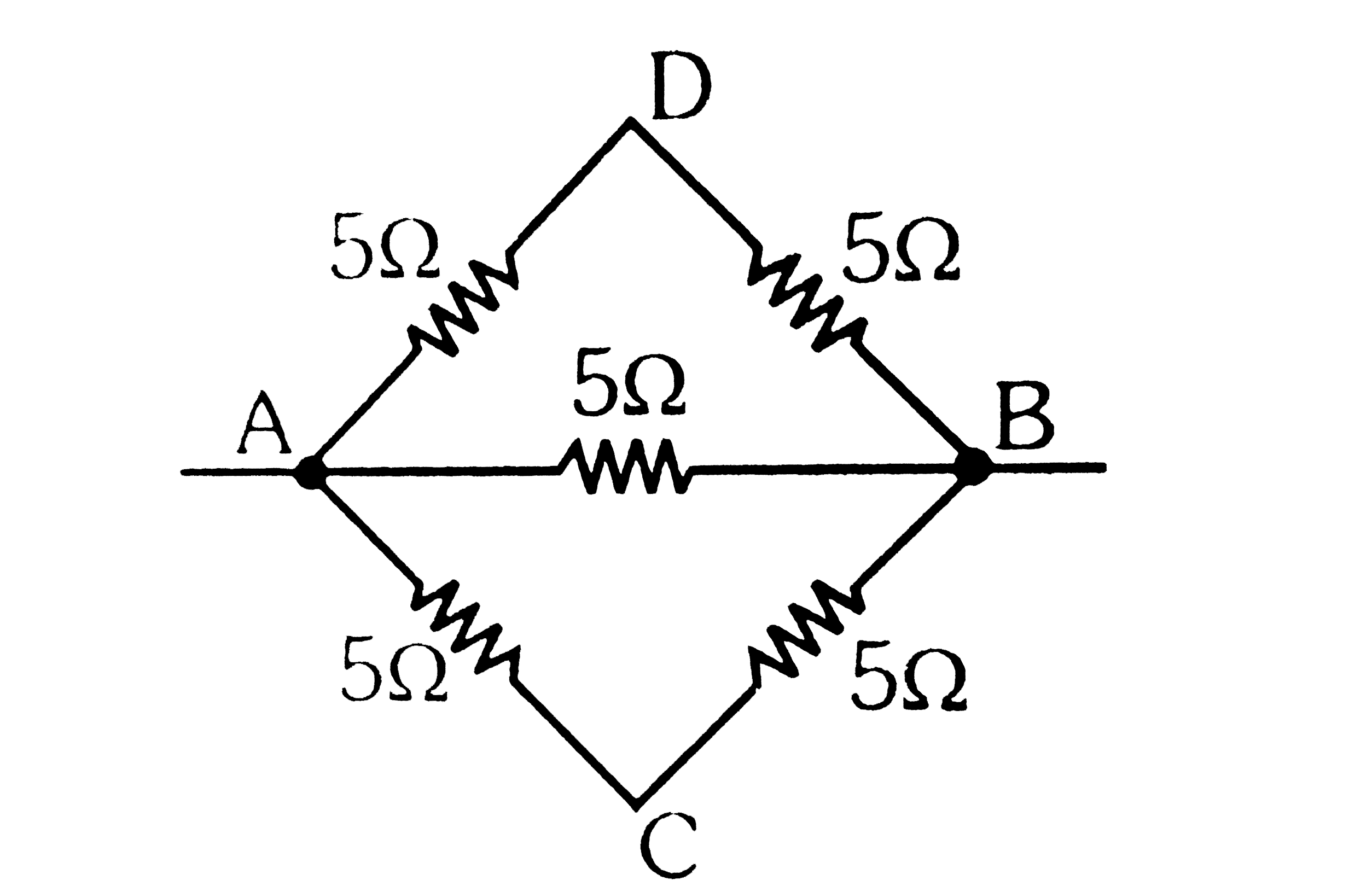 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω - Question 3 - Select One
In the infinite gride. If the value of r=2(√5−1)Ω. Find the Equivalent resistance between the point a and c.
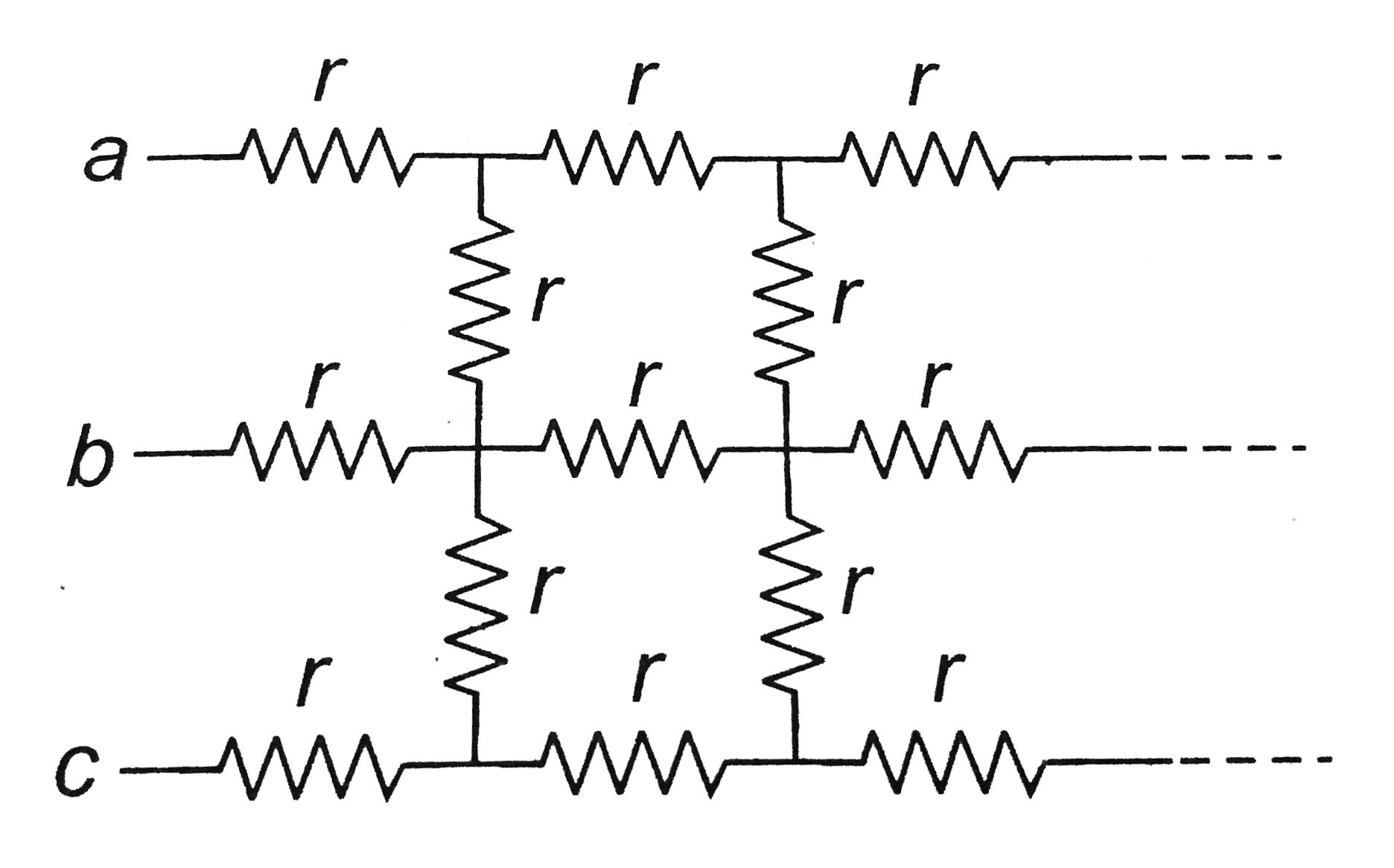 A6(√5−1)ΩB4(√5−1)ΩC4ΩDnone of these
A6(√5−1)ΩB4(√5−1)ΩC4ΩDnone of these
Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
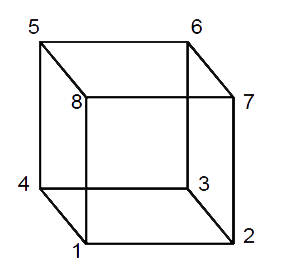
When current enters at 1 and leaves at 3View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
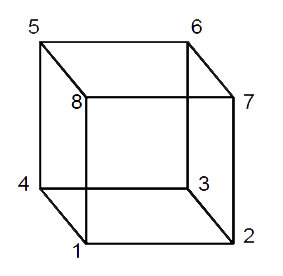
When current enters at 1 and leaves at 2View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
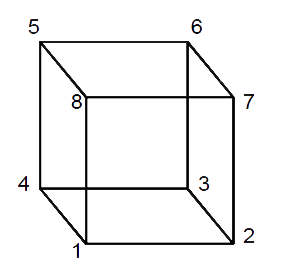
When current enters at 1 & leaves at 6 (body diagonal)View SolutionAll resistances in fig. 5.34 are in ohm. Find the effective resistance (in Ω) between points A and B.
 View Solution
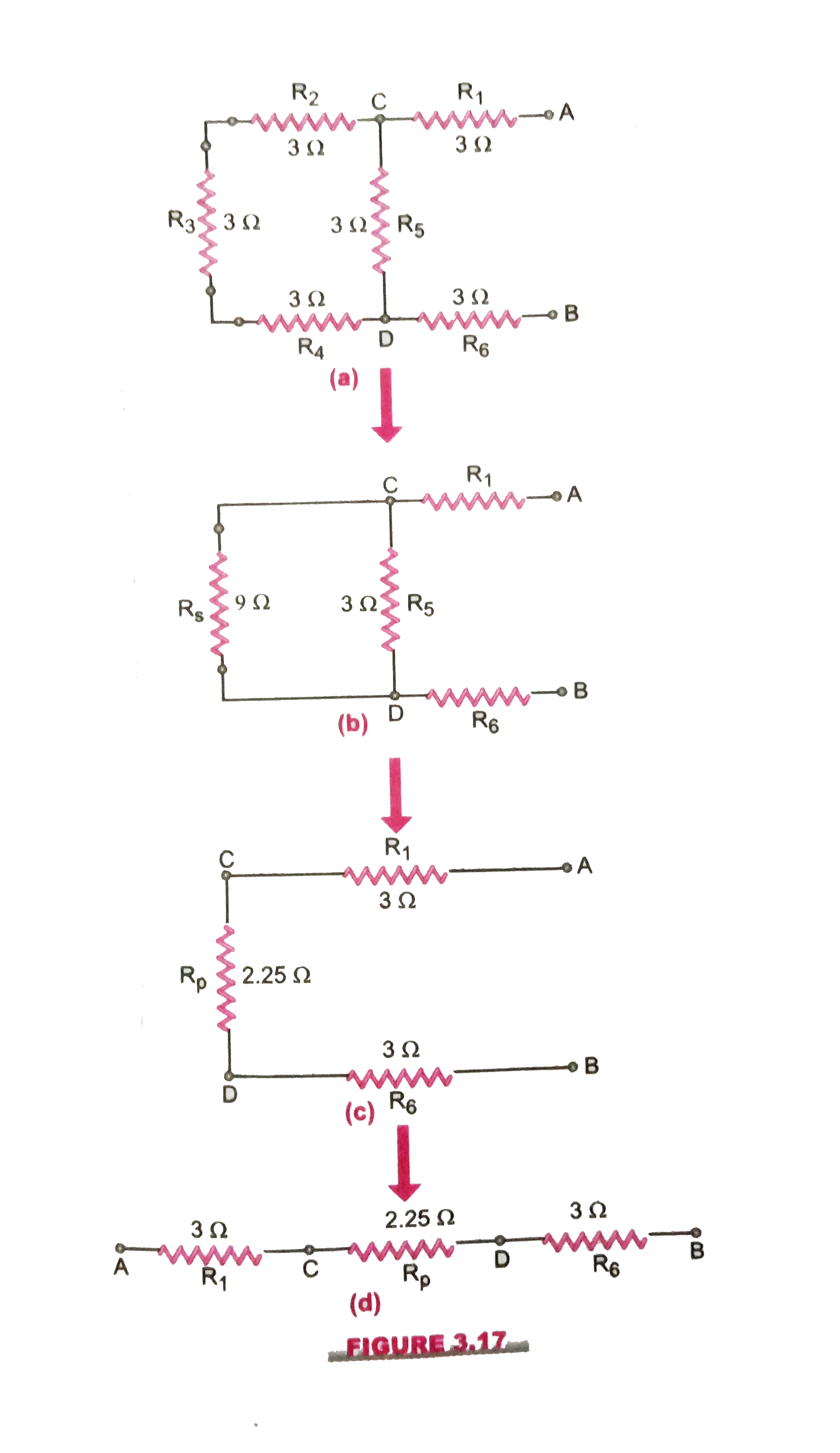
View SolutionFor the combination of resistors shown in (fig.)
(a) find the equivalent resistance between
(i) C and D and
(ii) A and B.
 .View Solution
.View Solution
