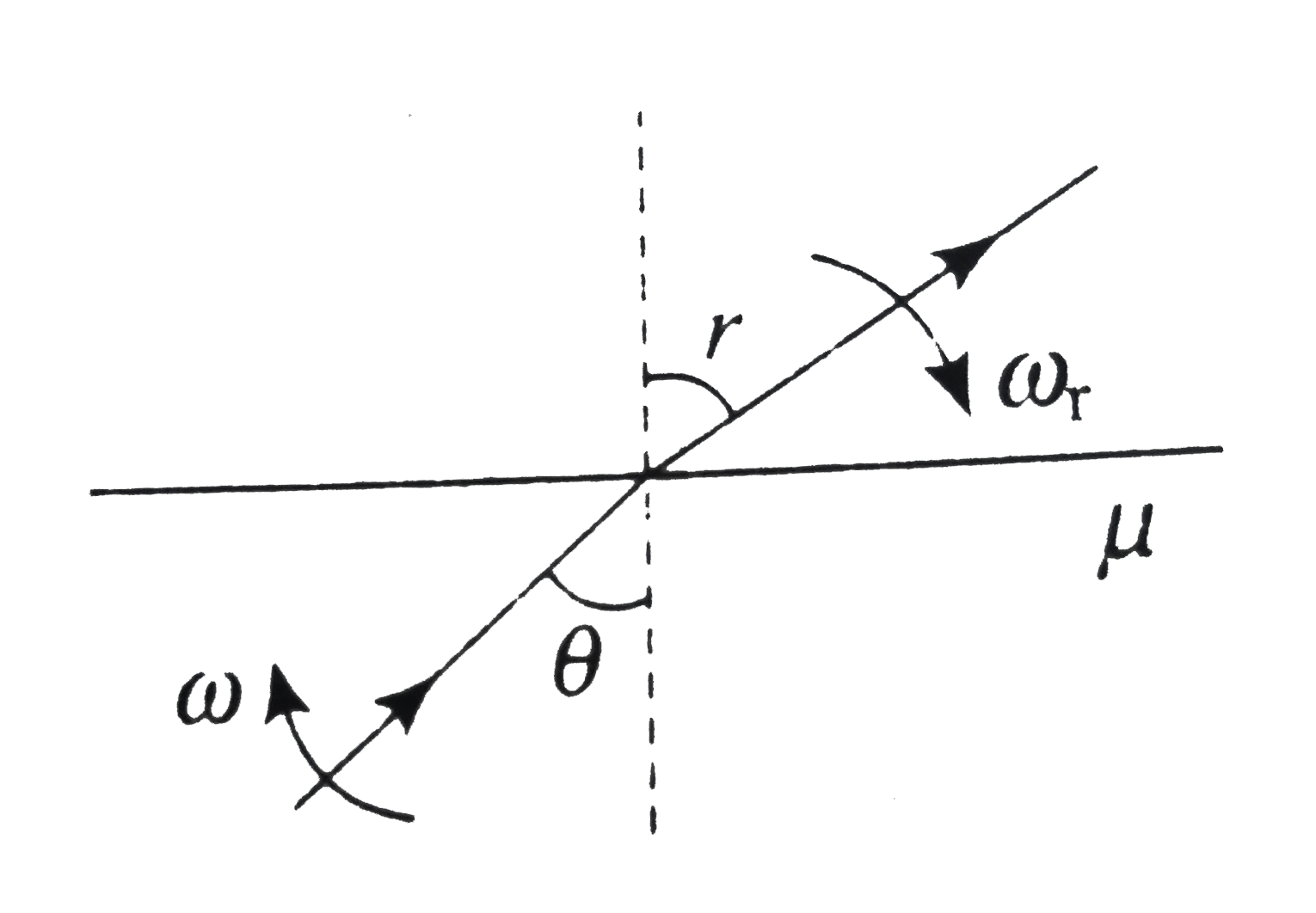
A ray of light ravels from a liquid of refractive index μ to air. If the incident beam is rotating at a rate ω , what is the angular sped of the refracted beam at the instant the angle of incidence is 30∘ ? (Given μ=√2,ω=1/√6rads−1).
sinr=μsinθ
For θ=30∘,μ=√2,
we get r=45∘
Differentiating (i), we get
cosr(drdt)=μcosθ(dθdt)
(cos45∘)ωr=√2(cos30∘)ω
ωr=√2(√3/2)(1√2)(1√6)=1√2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.412videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.522videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.220videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?View SolutionLight enters from vacuum to a medium of refractive index μ. If angle of incidence is double of angle of refraction, find angle of refraction.
View Solution
Knowledge Check
- Question 1 - Select One
A ray of light passes from glass having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
Asin−1(45)Bsin−1(35)Csin−1(58)Dsin−1(25) - Question 2 - Select One
A ray of light passes from vacuum of 3×108m/s medium of refractive index μ, the angle of incidence is found to be twice the angle of refraction. Then the angle of incidence is:
A2cos−1(μ2)Bsin−1(μ)Csin−1(μ2)Dcos−1(μ2) - Question 3 - Select One
A ray of light passes from vacuum of 3×108m/s medium of refractive index μ, the angle of incidence is found to be twice the angle of refraction. Then the angle of incidence is:
A2cos−1(μ2)Bsin−1(μ)Csin−1(μ2)Dcos−1(μ2)
A ray of light passes from glass, having a refractive indx of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
View SolutionThe ray of light travels from raer medium to denser medium of refractive index μ. The angle of incidence of twice the angle of refraction. The angle of incidence is given by
View SolutionA ray of light is incident on a medium of refractive index √2 at an angle of incidence of 45∘. The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
View SolutionA ray of light passes from vaccume into a medium of refractive index n. if the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA ray of light is travelling from glass to air. (Refractive index of glass =1.5). The angle of incidence is 50∘. The deviation of the ray is
View Solution
