A circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
The given loop may be obtained by the superposition of two
semicircular loops as shown in the figure.
The magnetic moment of the semicircle in the y-z plane is along
the x-axis and that in the x-z plane is along the y-axis.
Mx=πR2I2,My=πR2I2
The total magnetic moment is →M=Mxˆi+Myˆj
or M=πR2I2(ˆi+ˆj)

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example25videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank31videos
KINETIC THEORY
- BOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank50videos
Magnetism and Matter
Similar Questions
A conductor consists of a circular loop of radius R=10cm and two straight, long sections as shown in figure. The wire lies in the plane of the paper and carries a current of i=7.00A Determine the magnitude and direction of the magnetic field at the centre of the loop.
 View Solution
View SolutionTwo infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View Solution
Knowledge Check
- Question 1 - Select One
If a circular loop of wire of mass 'm' and radius 'R' is making 'n' revolutions per second about a point on its rim perpendicular to the plane of the loop, Then its rotational kinetic energy will be
Aπ2mR2n2B2π2mR2n2C4π2mR2n2D8π2mR2n2 - Question 2 - Select One
A circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
AπBr2t(1−π2)BπBr2t(1−π3)CπBr2t(1−π4)DπBr2t(1−π5) - Question 3 - Select One or More
A circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity ω. If resistance of the loop is R then current in the loop is
Azero, when θ=0Bπr2Bω2R when θ=0Cπr2Bω2R when θ=π6Dπr2Bω4R when θ=π6
A circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is
 View Solution
View SolutionThere is one circular loop of wire of radius R, carrying current I and magnetic field at its centre is B0, due to its own current. The loop is bent along its diameter at right angle. What will be the net magnetic field at the centre of the loop?
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View Solution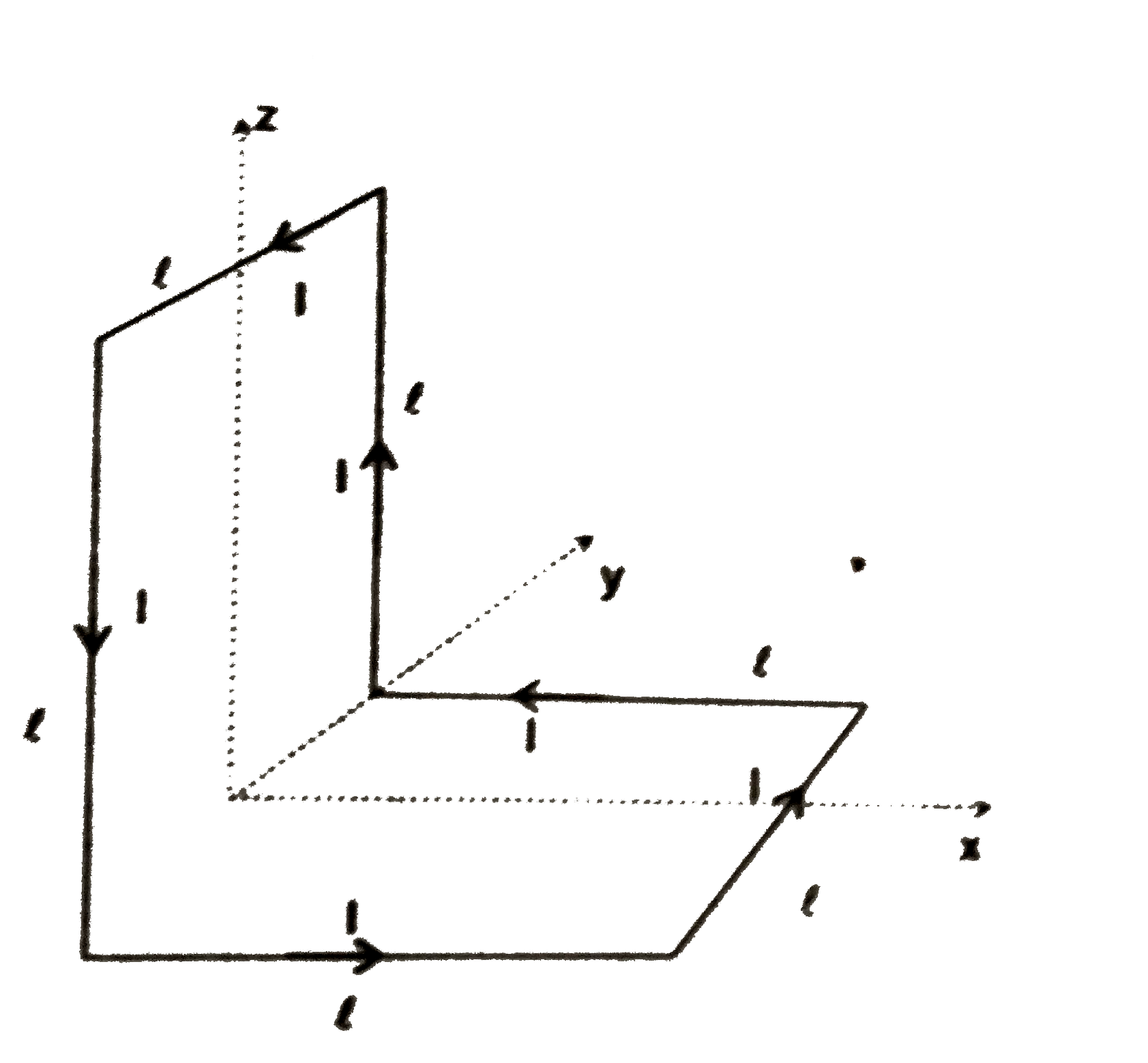
A conducting loop carrying current 'l' is bent into two halves and placed in mutually perpendicular planes xy and yz planes as shown. A uniform magnetic field →B=Bˆj is existing in the region. The net magnetic torque experienced by the loop isView SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
 View Solution
View Solution
