For the arrangement shown in Fig. determine the magnetic field at centre O.

Let current flowing through coil 1 be i1 and through coil 2 be i2.

Radius of each coil=R. Hence, magnetic field at O due to coil
1 is
→B1=μ0i12Rˆi
and magnetic field at O due to coil 2 is
→B2=μ0i22Rˆj
Therefore, net megnetic field →B=→B1+→B2
⇒→B=μ0i12Rˆi+μ0i22Rˆj
⇒∣∣→B∣∣=μ02R√i21+i22
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )10videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Practice Problems
- Question 1 - Select One
The magnetic field at centre , P will be
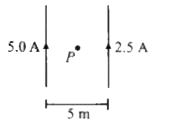 Aμ04πBμ0πCμ02πD4μ0π
Aμ04πBμ0πCμ02πD4μ0π - Question 1 - Select One
For the arrangment as shown in the figure, the magnetic induction at the centre is
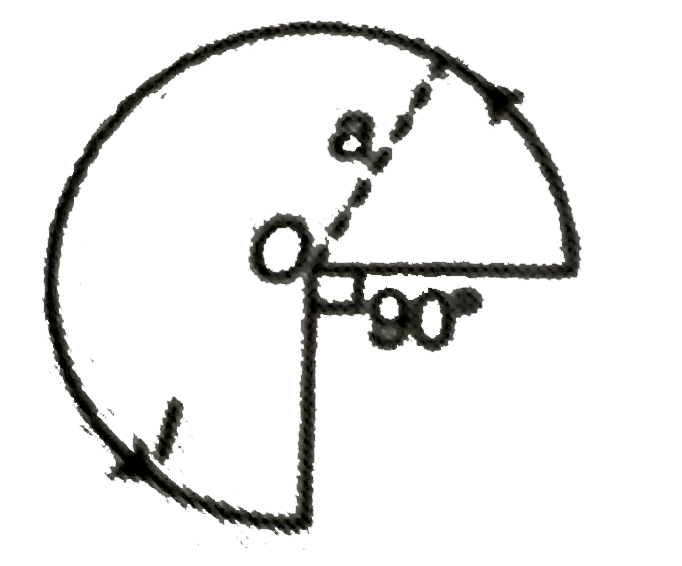 A3μ0Iπ4aBμ0I4πa(1+π)Cμ0I4πaD3μ0I8a
A3μ0Iπ4aBμ0I4πa(1+π)Cμ0I4πaD3μ0I8a - Question 1 - Select One
In the given loop the magnetic field at the centre O is
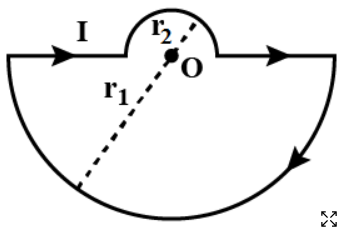 AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the page
AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the page - Question 1 - Select One
The magnetic induction at centre O Fig.
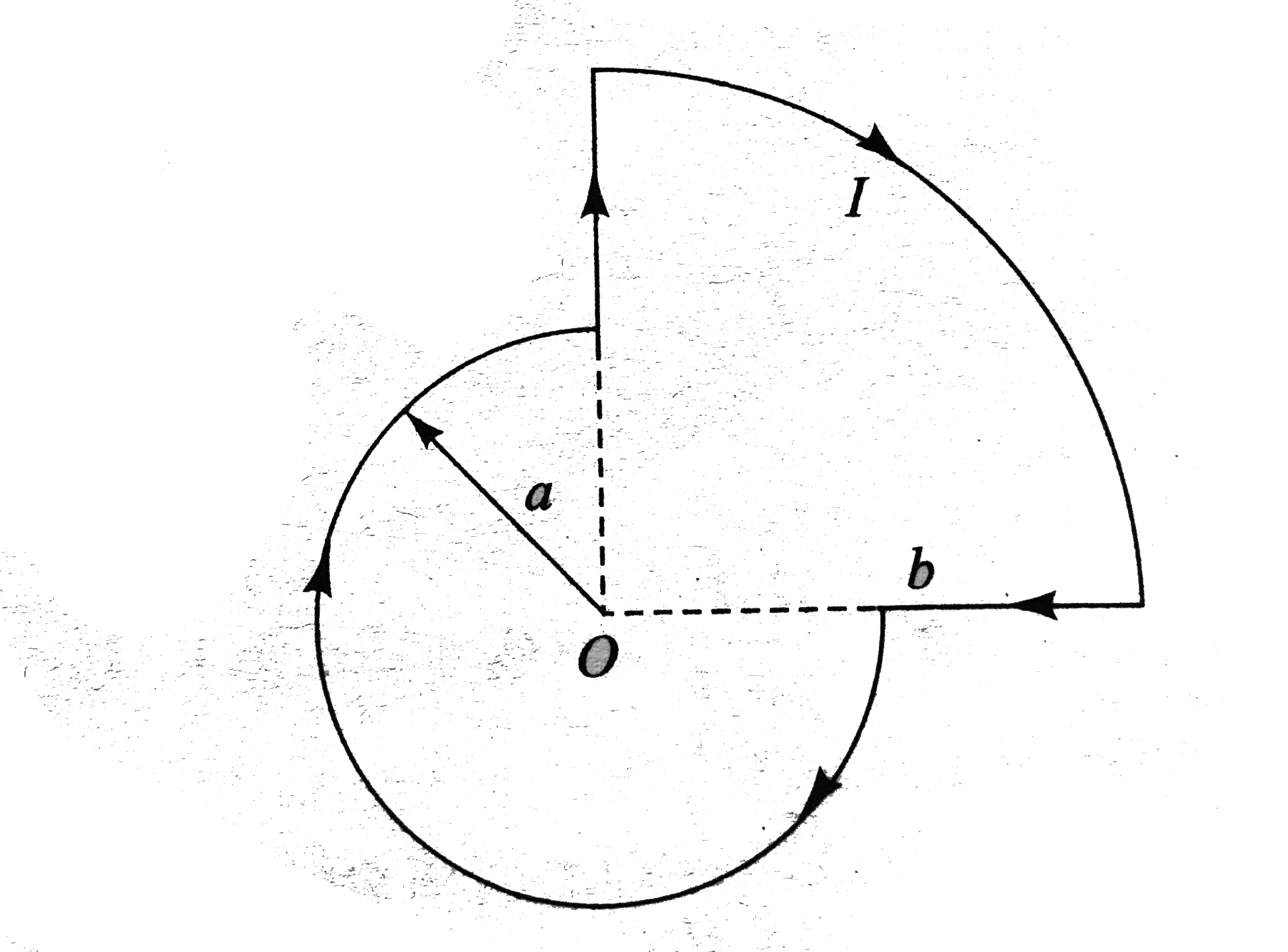 Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙
Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙ - Question 1 - Select One
The resistances of three parts of a circular loop are as shown in Fig. The magnetic field at the centre O is (current enters at A and leaves at B and C as shown)
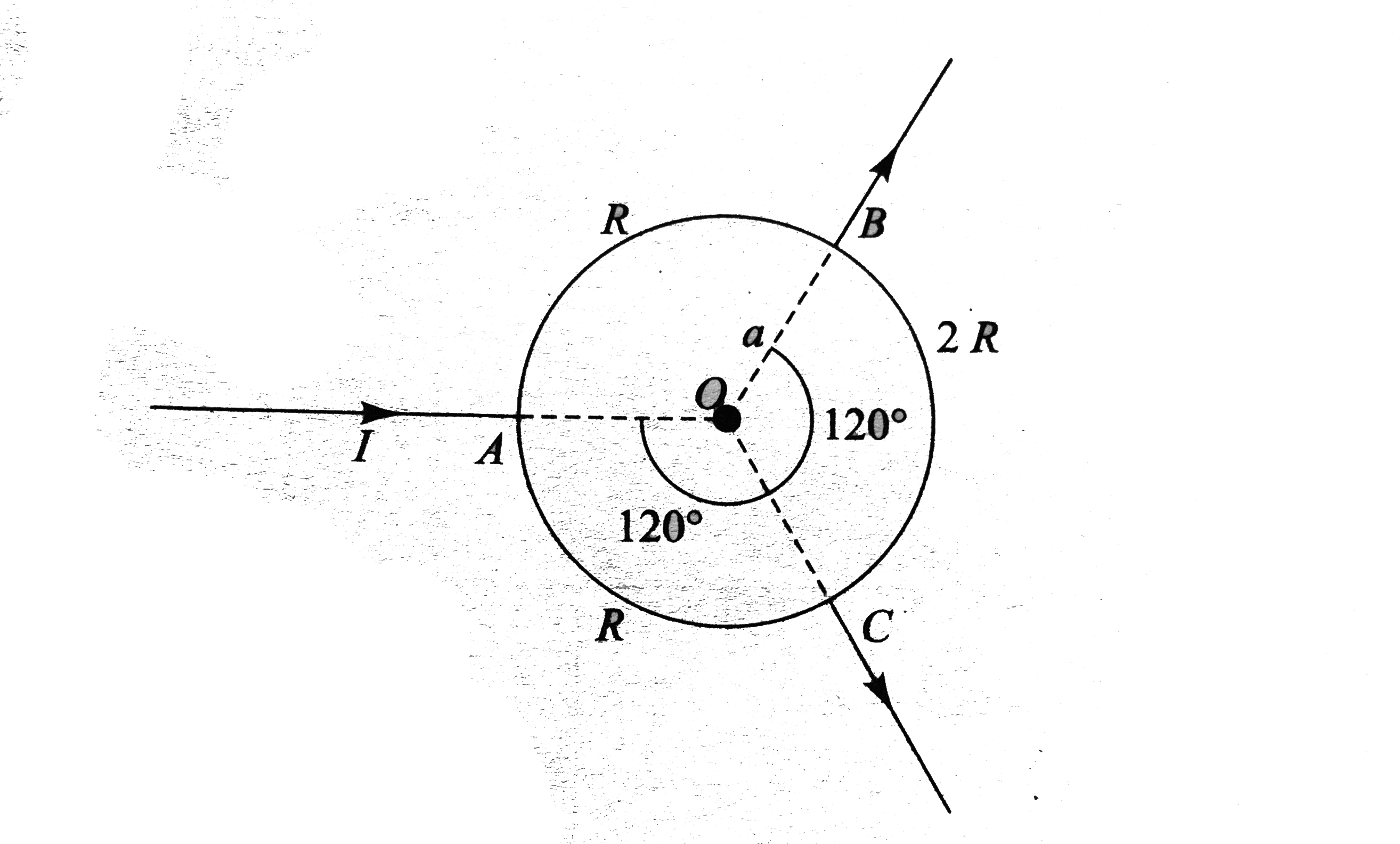 Aμ0I6aBμ0I3aC23μ0IaDzero.
Aμ0I6aBμ0I3aC23μ0IaDzero.
Similar Questions
In Fig. Find the magnetic field at common centre.
 View Solution
View SolutionIn Fig, find the magnetic field at point P.
 View Solution
View SolutionIn the net work shown in figure,find the magnetic field at the centre O of the coil.
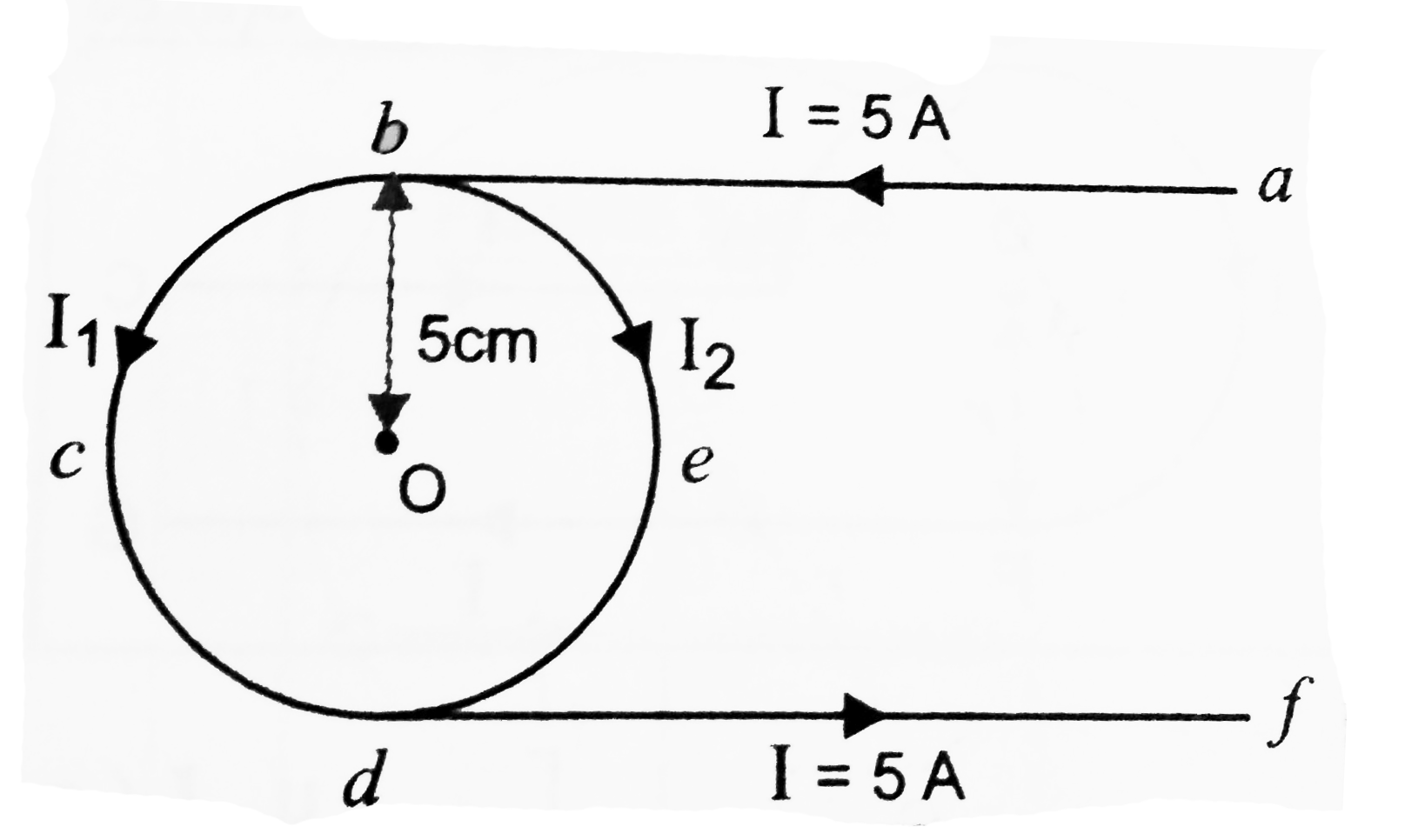 View Solution
View SolutionA current I enters a uniform circular loop of radius R at point M and flows out at N as shown in the Fig. Obtain the net magnetic field at the centre O of the loop.
View SolutionThree identical long solenoid P,Q and R are connected to each other as shown in fig. If the magnetic field at the centre of P is 2.0T, what would be the field (inT) at the centre of Q? Assume that the field due to any solenoid is confined within the volume of that solenoid only.
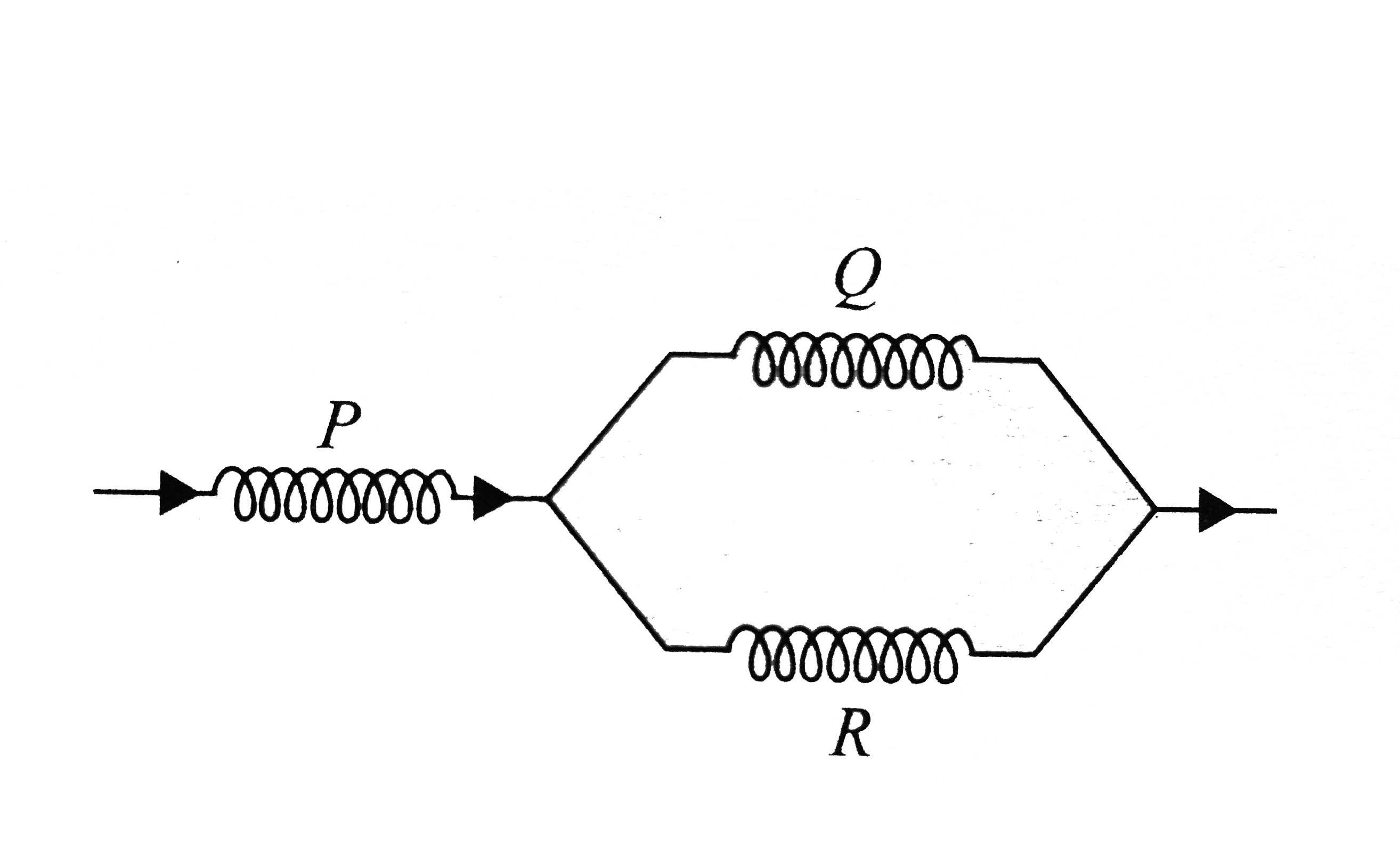 View Solution
View Solution

