A coil carrying a steady current is short-circuited. The current in it decreases α times in time t0. The time constant of the circuit is
A
τ=t0 In α
B
τ=t0Inα
C
τ=t0α
D
τ=t0α−1
Video Solution
Text Solution
The correct Answer is:B
I=I0α at t=t0
Since I=I0e−t0/τ⇒1α=e−t0/τ
α=e−t0/τ⇒t0=τlogeα
τ=t0logeα
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit28videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank31videos
KINETIC THEORY
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T).
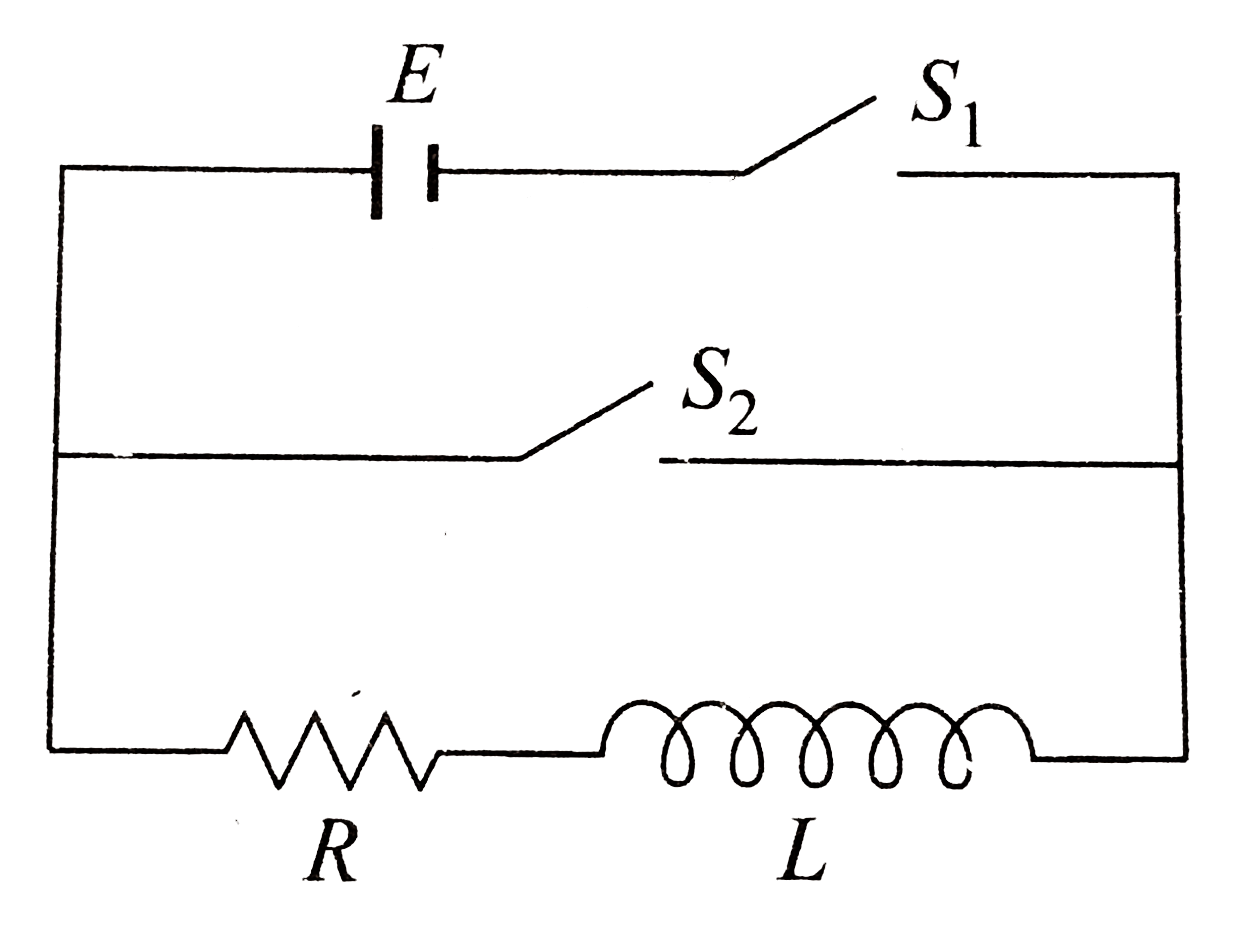
When a coil carrying a steady current is short circuited, the current decreases in it η times in time t0. The time constant of the circuit isAt01nηBt01nηCt0ηDt0η−1 - Question 2 - Select One
When a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
ATβBTln(1β)CTlnβDTlnβ - Question 3 - Select One
At the time of short-circuit, the current in the circuit:
A(a) reduces substantiallyB(b) does not changeC(c) increases heavilyD(d) varies continuously.
At the time of short circuit, the current in the circuit
View SolutionAt the time of short circuit, the current in the circuit :
View SolutionAt the time of short circuit, the current in the circuit
View SolutionAt the time of short circuit, the current in the circuit :
View SolutionAt the time of short circuit, the current in the circuit :
View Solution
