If i1=3sinωtand(i2)=4cosωt, then (i3) is

A
5sin(ωt+53∘)
B
5sin(ωt+37∘)
C
5sin(ωt+45∘)
D
5sin(ωt+35∘)
Video Solution
Text Solution
The correct Answer is:A
(i3)=(i1)+(i2)=3sinωt+4cosωt
=3sinωt+4sin(ωt+90∘)
(i30)=√I210+I220=√32+42=5
tan(ϕ)=43⇒ϕ=53∘
so, (i_3)=(I_(30) sin(omega t+phi)=5 sin (omega t+53^(@)).

|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct5videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning7videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective15videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - OSCILLATIONSEXERCISE - QUESTION BANK39videos
OSCILLATIONS
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
Knowledge Check
- Question 1 - Select One
In the given figure, if i1=3sinωtandi2=4cost, then i3 is
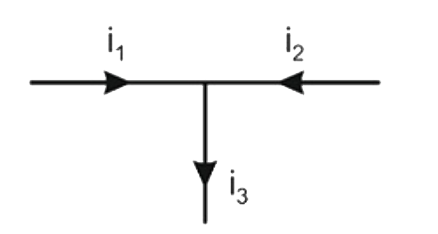 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5cos(ωt+53∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5cos(ωt+53∘) - Question 1 - Select One
Two wave are represented by equation y1=asinωt and y2=acosωt the first wave :-
Aleads the second by πBlags the second by πCleads the second by π2Dlags the second by π2 - Question 1 - Select One
The ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
A√2B1√2C1D2 - Question 1 - Select One
The displacements of two intering lightwaves are y1=4sinωt and y2=3cos(ωt). The amplitude of the resultant wave is (y1 and y2 are in CGS system)
A5 cmB7 cmC1 cmDzero - Question 1 - Select One
Find the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωtA5B10C15D20 - Question 1 - Select One
If i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
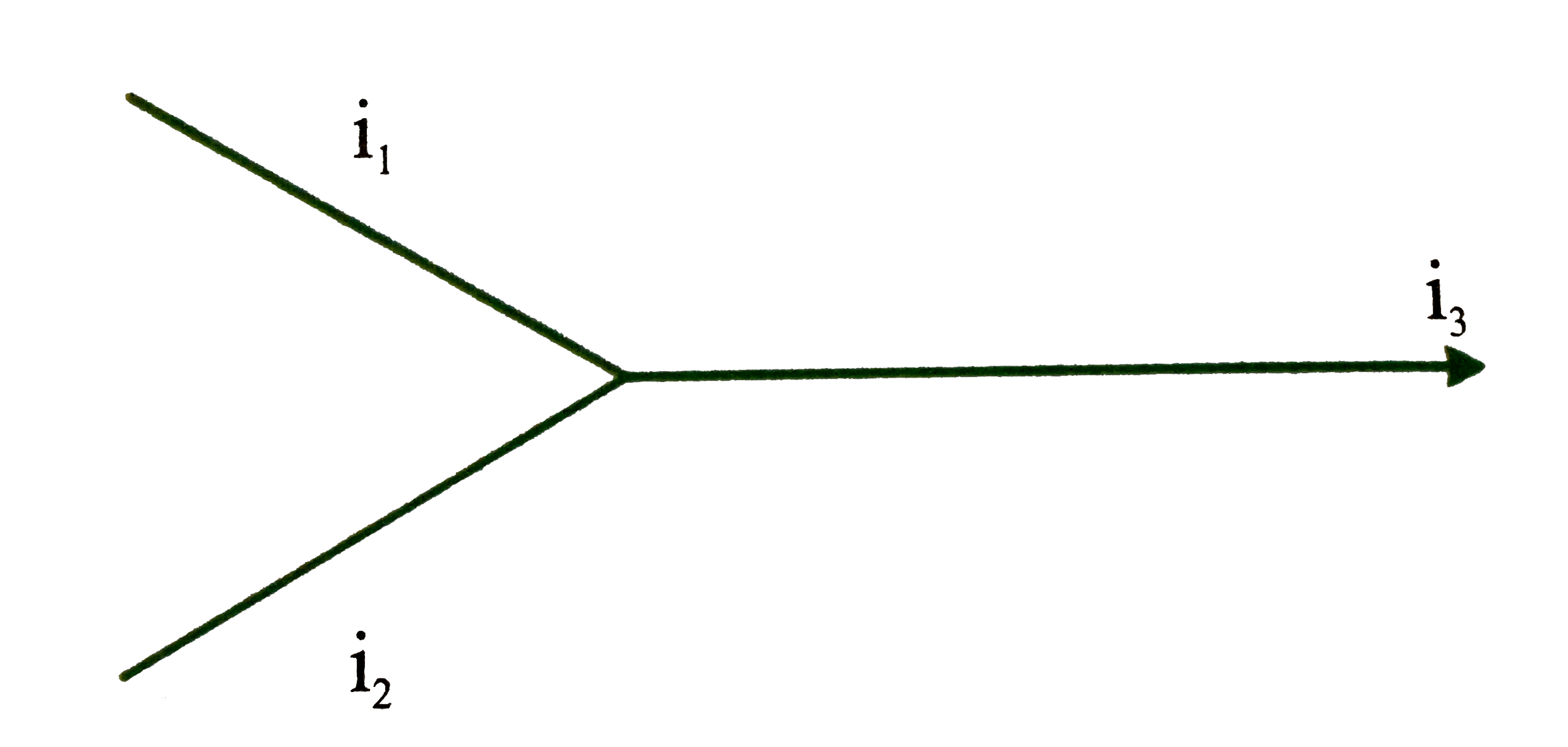 A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
Similar Questions
If i1=3sinωt and i2=6cosωt, then i3 is
 View Solution
View Solutionx1=3sinωt,x2=4cos'ωt Find (i) amplitude of resultant SHM. (ii) equation of the resultant SHM.
View Solutionx1=3sinωt,x_(2) = 4 cos omega t
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.View Solutionx1=3sinωt⇒x2=4cosωt. Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.
View Solution

