In the previous problem, the maximum range of movement of the centre of the part of the circle from line AD in which charged particle of charge Q moves with a velocity v when $(θ)$ is positive to when $(θ)$ is negative is given by

A

$\pm \frac{m v}{2 Q B}$

B

$\pm \frac{m v}{Q B}$

C

$\pm \frac{2 m v}{Q B}$

D

$\pm \frac{2 m v}{3 Q B}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

An observation will show that when $θ$ is positive and actually $90^{\circ}$ angle formed will be $2 π$ at the center and centre of the circle formed by the charged particle will be at a distance of radius of the circle from AD.
It will be also true for $θ$ to be negative. ( $θ$ measured anticlockwise form normal AC).
Hence range is $\pm r = \pm \frac{m v}{Q B}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

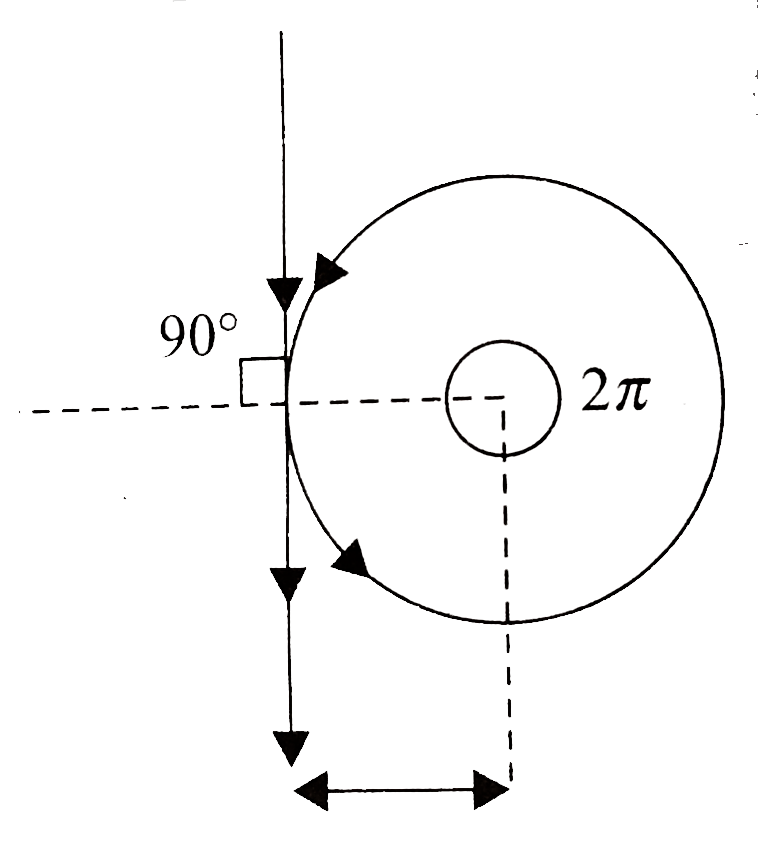
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the previous problem, if time period, $T = 2 (π) \frac{m}{B Q}$ where Q is the charge of the particle and m is its mass, the ratio of time spent by the particle in field when $(θ)$ is positive to when $(θ)$ is negative is given by
A $(\frac{π / 2 + θ}{π / 2 - θ})$
B $(\frac{π + θ}{π - θ})$
C $(\frac{π - θ}{π + θ})$
D $(\frac{π / 2 - θ}{π / 2 + θ})$
Question 2 - Select One
The force acting on a particle of charge q moving in a uniform magnets field with velocity v is
Aparallel to both $\to v$ and $\to B$
Bperpendicular to both $\to v$ and $\to B$
Cparallel to $\to v$ and perpendicular to $\to B$
Dperpendicular to $\to v$ and parallel to $\to B$
Question 3 - Select One
A charged particle of charge $Q$ and mass $m$ moves with velocity $v$ in a circular path due to transverse magnetic field, B, then its frequency is
A $\frac{Q B}{2 π m}$
B $\frac{Q v B}{2 π m}$
C $\frac{Q m v B}{2 π}$
D $\frac{v b}{2 π Q m}$

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Integer

Home
Ask Doubt
Profile