The magnitude of gratitational field intensities at distance r1 and r2 from the centre of a uniform solid sphere of radius R and mass M are I1 and I2 respectively. Find the ratio of I1/I2 if (a) r1>R and r2>R and (b) r1<R and r2<R (c ) r1>R and r2<R.
Video Solution
Text Solution
Gravitational field intensity for a uniform spherical distribution of mass is given by :
I=GMr2 for r>R and
=GMR3r for r<R.
(a) r1>R and r2>R
I1I2=(GM/r21)(GM/r22)=r22r21
(b) r1<R and r2<R
I1I2=(GM/R3)r1(GM/R3)r2=r1r2
(c ) r1>R and r2<R
I1I2=(GM/r21)(GM/R3)r2=R3r21r2
|
Updated on:21/07/2023
Related Playlists
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Solved Example8videos
GRAVITATION
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Practice Exercise18videos
GRAVITATION
- BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)8videos
CENTRE OF MASS & MOMENTUM CONSERVATION
- BOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise89videos
HEAT TRANSFER
Similar Practice Problems
- Question 1 - Select One
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 if r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r22r32 if r1<R and r2<RDE1E2=r21r22 if r1<R and r2<R - Question 1 - Select One
The magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
AF1F2=r1r2 if r1>R and r2<RBF1F2=r22r21 if r!>R and r2>RCF1F2=r31r32 if r1<R and r2<RDF1F2=r21r22 if η<R and r2<R - Question 1 - Select One
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 ir r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r31r32 if r1<R and r2<RDE1E2=r21r22 ir r1<R and r2<R - Question 1 - Select One
The magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M and F1 and F2 respectively. Then,
AF1F2=r1r2ifr1<R and r2<RBF1F2=r21r22ifr1>R and r2>RCBoth (a) and (b)DNone of the above - Question 1 - Select One
The magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M and F1 and F2 respectively. Then,
AF1F2=r1r2ifr1<R and r2<RBF1F2=r21r22ifr1>R and r2>RCBoth (a) and (b)DNone of the above - Question 1 - Select One
Two loops P and Q are made from a uniform wire. The redii of P and Q are r1andr2 respectively, and their moments of inertia are I1andI2 respectively, IfI2=4I1,thenr2r1equals-
A42/3B41/3C4−2/3D4−1/3 - Question 1 - Select One
Two loops P and Q are made from a uniform wire. The redii of P and Q are r1andr2 respectively, and their moments of inertia are I1andI2 respectively, IfI2=4I1,thenr2r1equals-
A42/3B41/3C4−2/3D4−1/3 - Question 1 - Select One
Two loops P and Q are made from a uniform wire. The redii of P and Q are r1andr2 respectively, and their moments of inertia are I1andI2 respectively, IfI2=4I1,thenr2r1equals-
A423B413C4−23D4−13 - Question 1 - Select One
In the given circuit if I1 and I2 be the current in resistance R1 and R2 respectively then:
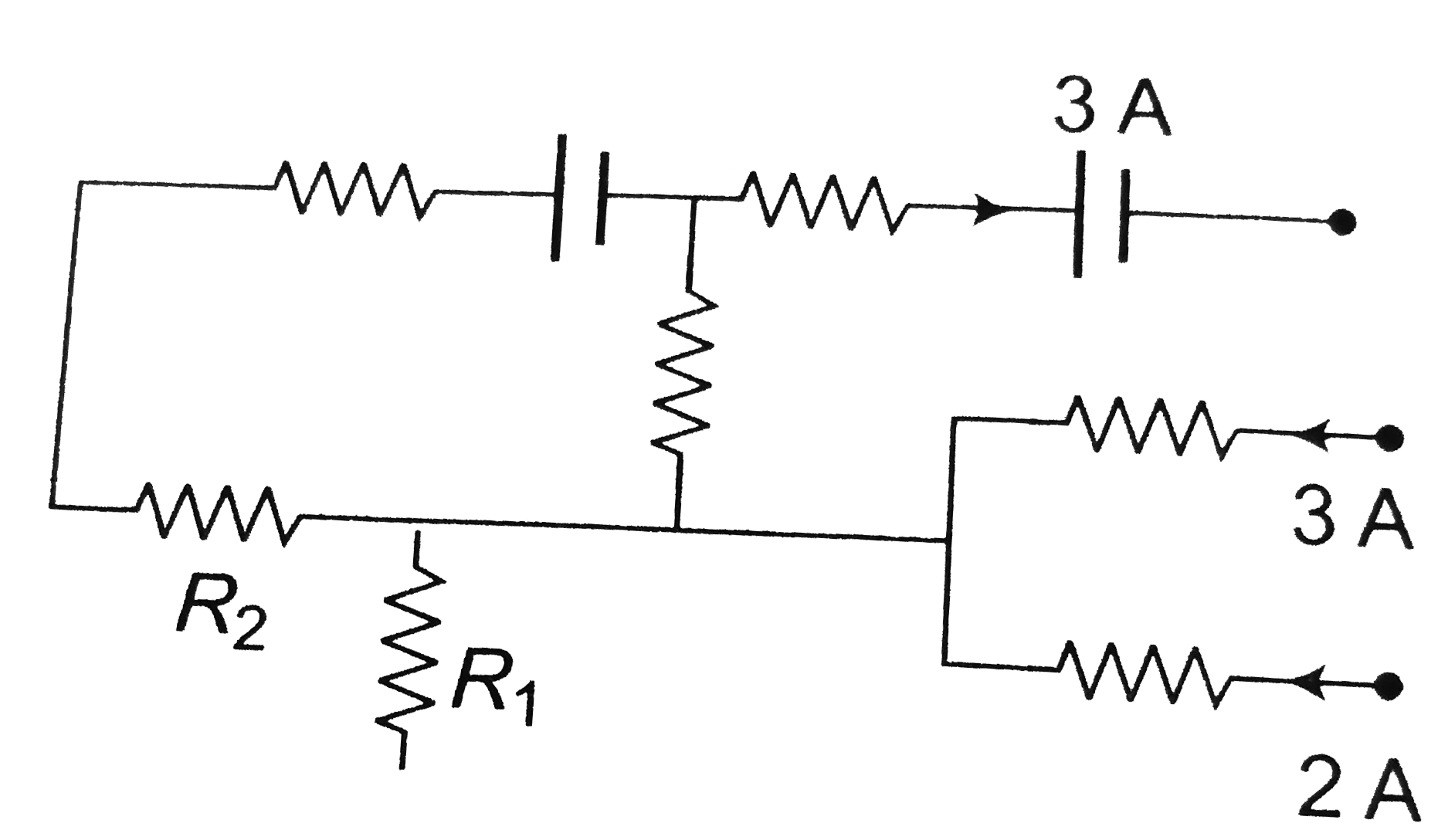 AI1=3A,I2=2ABI1=0,I2=2ACI1=2A,I2=2ADI1=2A and I2 can’t be determined with given data
AI1=3A,I2=2ABI1=0,I2=2ACI1=2A,I2=2ADI1=2A and I2 can’t be determined with given data

