A vertical tower, OP stands at the center O of a square ABCD. Let h and b denote the length OP and AB respectively. If ∠APB=60∘, what is the relationship beween h and b?
A
2b2=h2
B
2h2=b2
C
3b2=2h2
D
3h2=2b2
Text Solution
The correct Answer is:B
|
Updated on:21/07/2023
Related Playlists
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In32videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST24videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE6videos
COMPLEX NUMBERS
Knowledge Check
- Question 1 - Select One
A tower of height h stands at a point O on the ground. Two poles of height a and b stand at the points A and B respectively such that O lies on the line joining A and B. If the angle of elevation of the top of the tower at the foot of one pole is ame as at the top of the other pole, then h is equal to
Aa+babBaba+bCa + bDa+b|a−b| - Question 1 - Select One
A tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
Aa√3B√3aC2a√3D2√3a - Question 1 - Select One
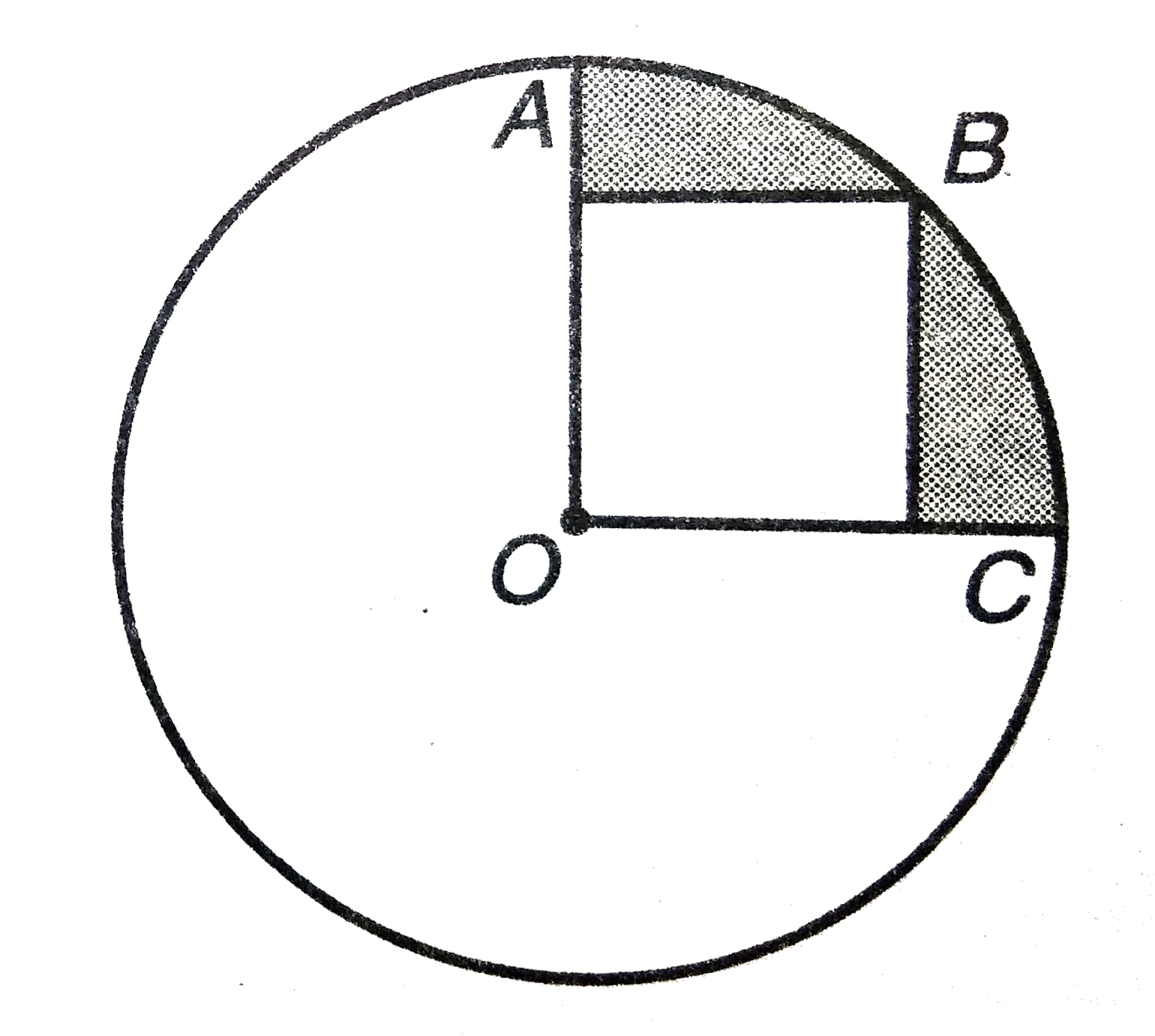
In the figure above, OABC is a square and B is a points on the circle with center O. If AB=6, what is the area of the shaded region?A9(π−2)B9(π−1)C12(π−2)D18(π−2) - Question 1 - Select One
A tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
A2a√3B2a√3Ca√3Da√3 - Question 1 - Select One
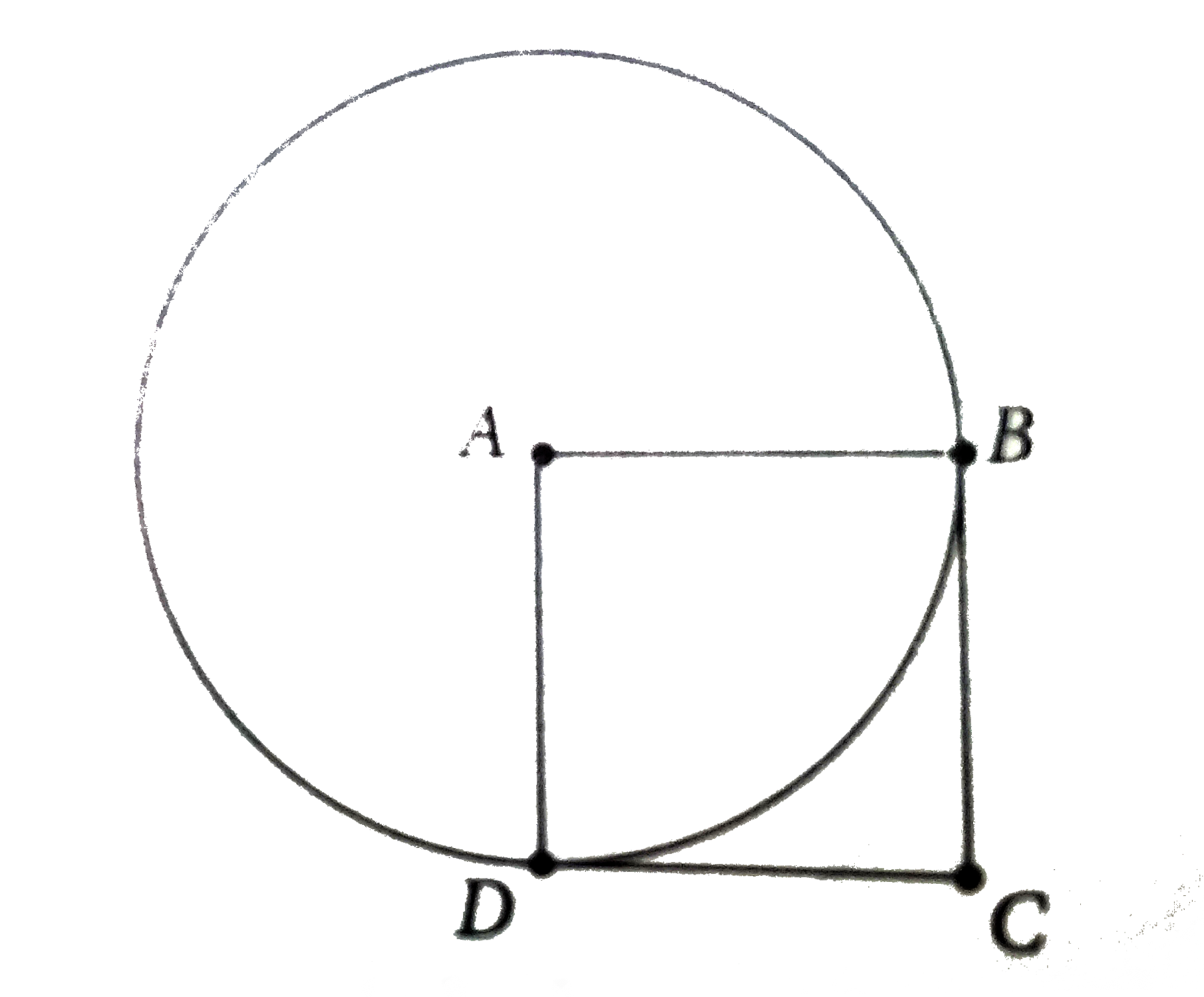
Points D and B lie on the circle above with center A. If square ABCD has an area of 16, what is the length of arc BD?A4B2πC8D4π - Question 1 - Select One
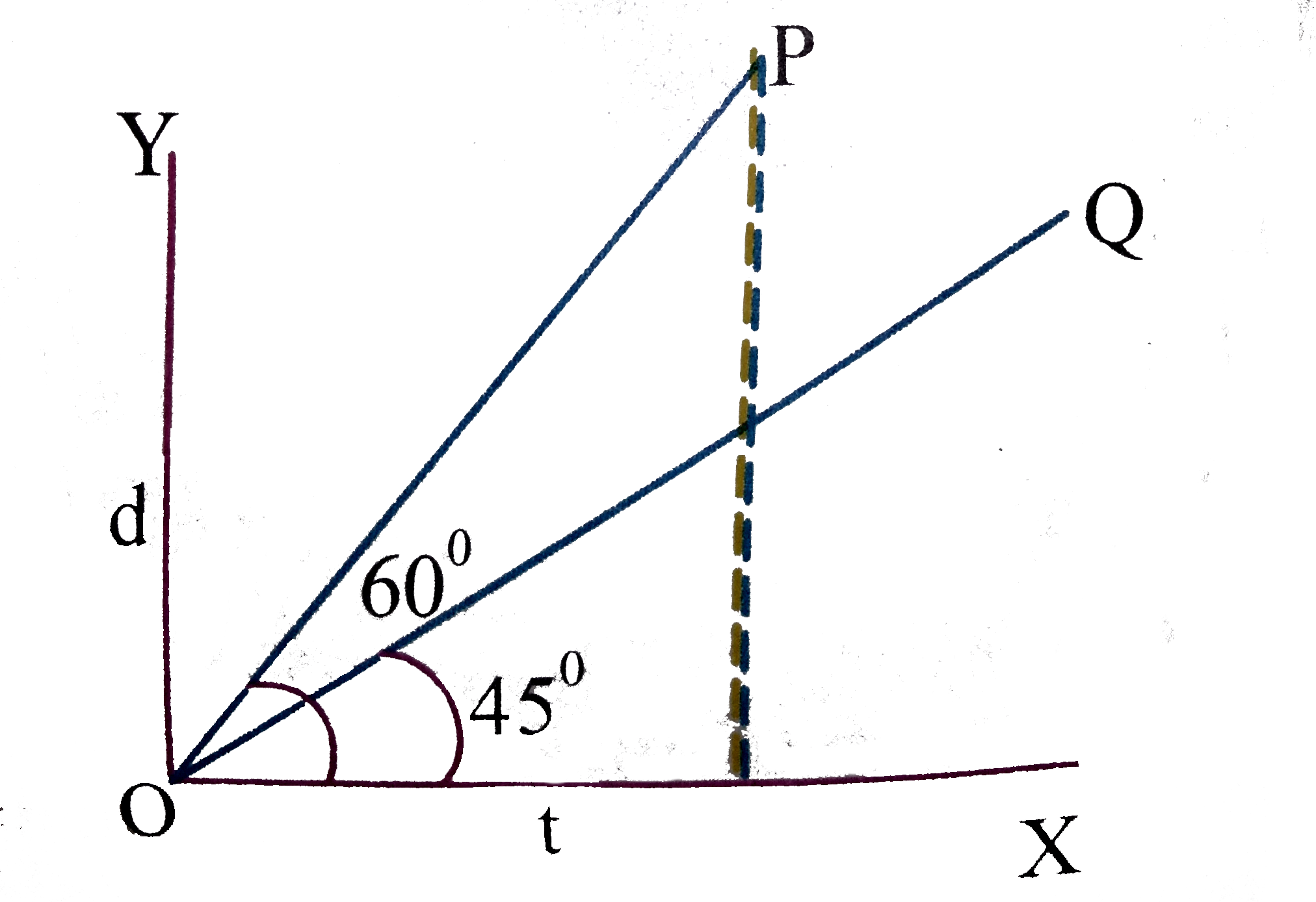
The displacement-time graphs of two bodies A and B are OP and OQ respectively. If ∠POX is 60∘ and ∠QOX is 45∘ the ratio of the velocity of A to that of B isA√3:√2B√3:1C1:√3D3:1
Similar Questions
The centre of a circle is at O. AB and CD are two chordsof length dande respectively. If P is the mid point of CD, then the length OP is:
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.
 View Solution
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.
 View Solution
View Solution

