The area of the portion of the circle x2+y2=1 which lies inside the parabola y2=1−x, is -
A
π2−23
B
π2+23
C
π2+43
D
π2−43
Video Solution
Text Solution
The correct Answer is:C
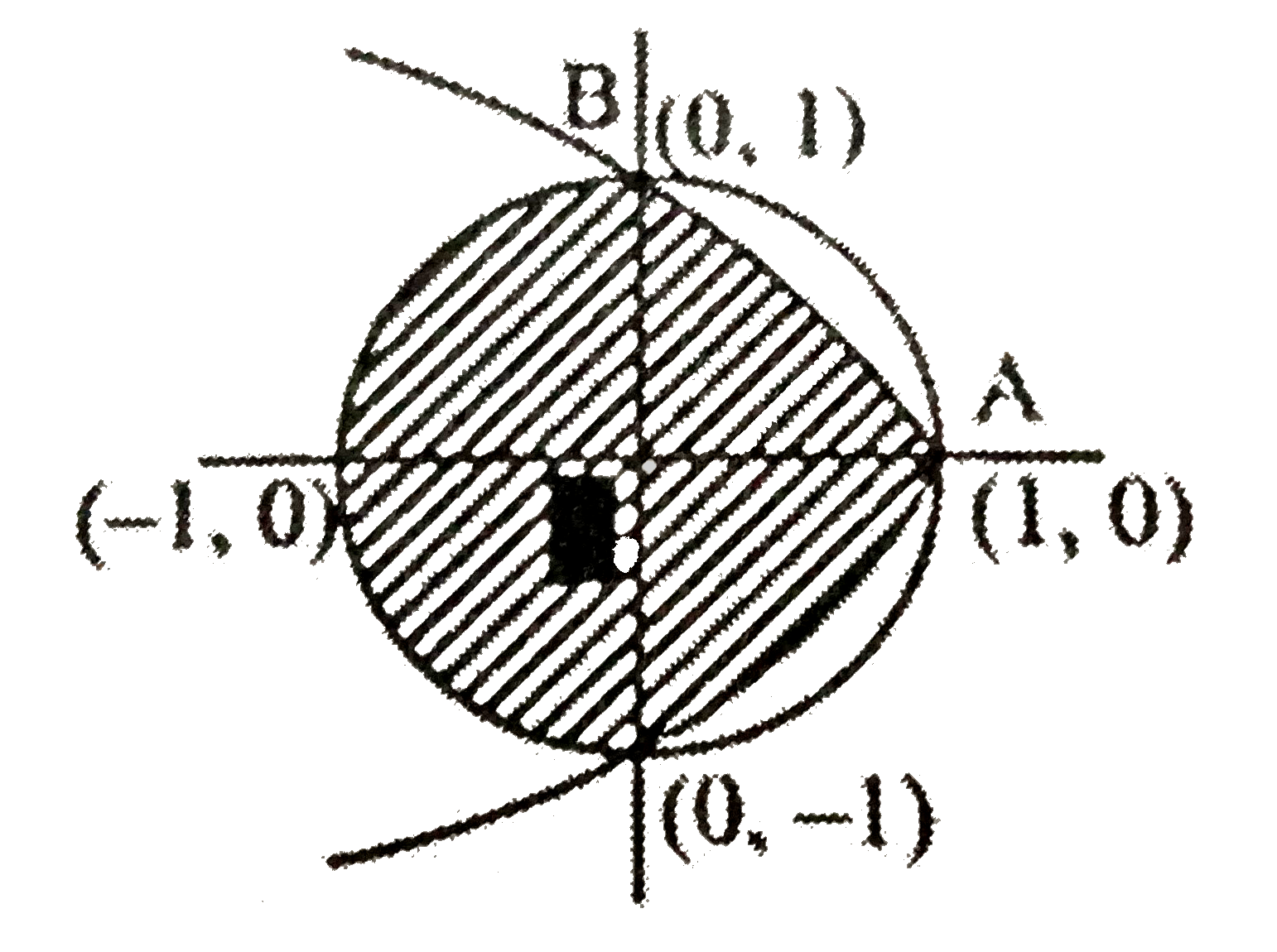
Area = semicircle +2 (area of are OAB)
π×122+21∫0√1−xdx=π2−2((1−x)3/23/2)10
=π2+43
|
Updated on:21/07/2023
Related Playlists
Similar Practice Problems
- Question 1 - Select One
The area of the portion of the circle x2+y2=64 which is exterior to the parabola y2=12x is
A(8π−√3)squnitsB163)(8−√3)squnitsC163)(8π−√3)squnitsDnone of the above - Question 1 - Select One
The area of the portion of the circle x2+y2=64 which is exterior to the parabola y2=12x is
A(8π−√3)squnitsB163)(8−√3)squnitsC163)(8π−√3)squnitsDnone of the above - Question 1 - Select One
The area ( in sq, units ) of the part of the circle x2+y2=36 , which is outside the parabola y2=9x, is
A24π+3√3B12π−3√3C24π−3√3D12π+3√3 - Question 1 - Select One
No portion of the circle x2+y2−16x+18y+1=0 lies in the
Afirst quadrntBsecond quadrantCthird quadrantDfourth quadrant
Similar Questions
Find the area of that part of the circle x2+\ y2=16 which is exterior to the parabola y2=6x.
View SolutionFind the area of the semi-portion of the circle x2+y2=4.
View SolutionThe area of the portion of the circle x2+y2−4y=0 lying below the x -axis is
View SolutionFind the area of the circle 4x2+4y2=9 which is interior to the parabola x2=4y.
View SolutionFind the area of circle 4x2+4y2=9 which is interior to the parabola x2=4y
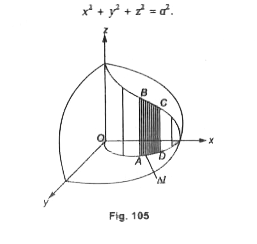
View SolutionCompute the area of the portion of the cylinder surface x2+y2=ax situated inside the sphere
x2+y2+z2=a2
 View Solution
View Solution

