AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
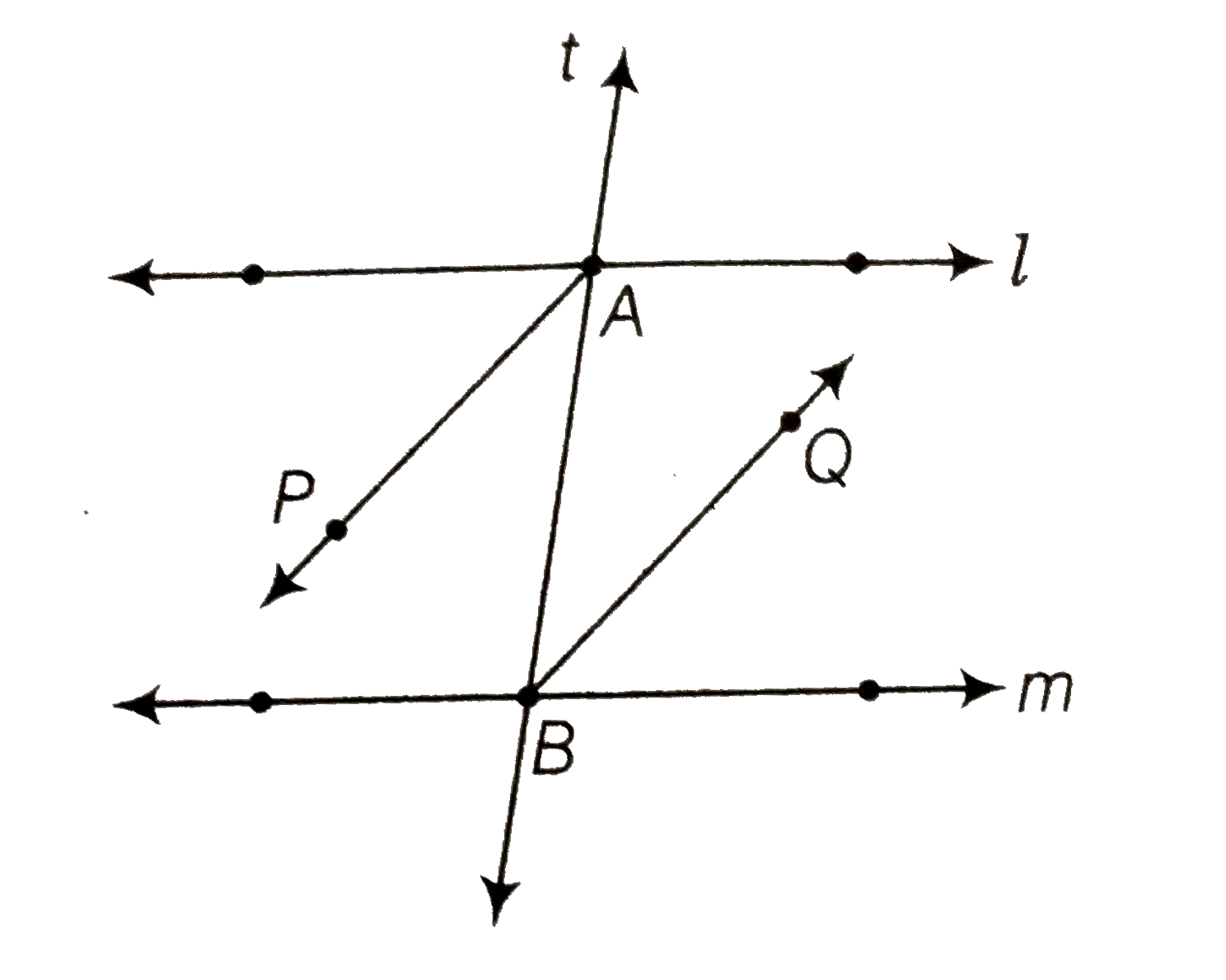
Given In the figure l||m , AP and BQ are the bisectors of ∠EAB and ∠ABH, respectively.
To Prove AP|| BQ
Proof Since, l||m and t is transversal.
Therefore, ∠EAB=∠ABH [alternate interior angles]
⇒ 12∠EAB=12∠ABH [dividing both sides by 2]
⇒ ∠PAB=∠ABQ [AP and BQ are the bisectors of ∠EABand∠ABH]
Since, ∠PAB and ∠ABQ are alternate interior angles with two lines AP and BQ and transversal AB, Hence, AP || BQ.
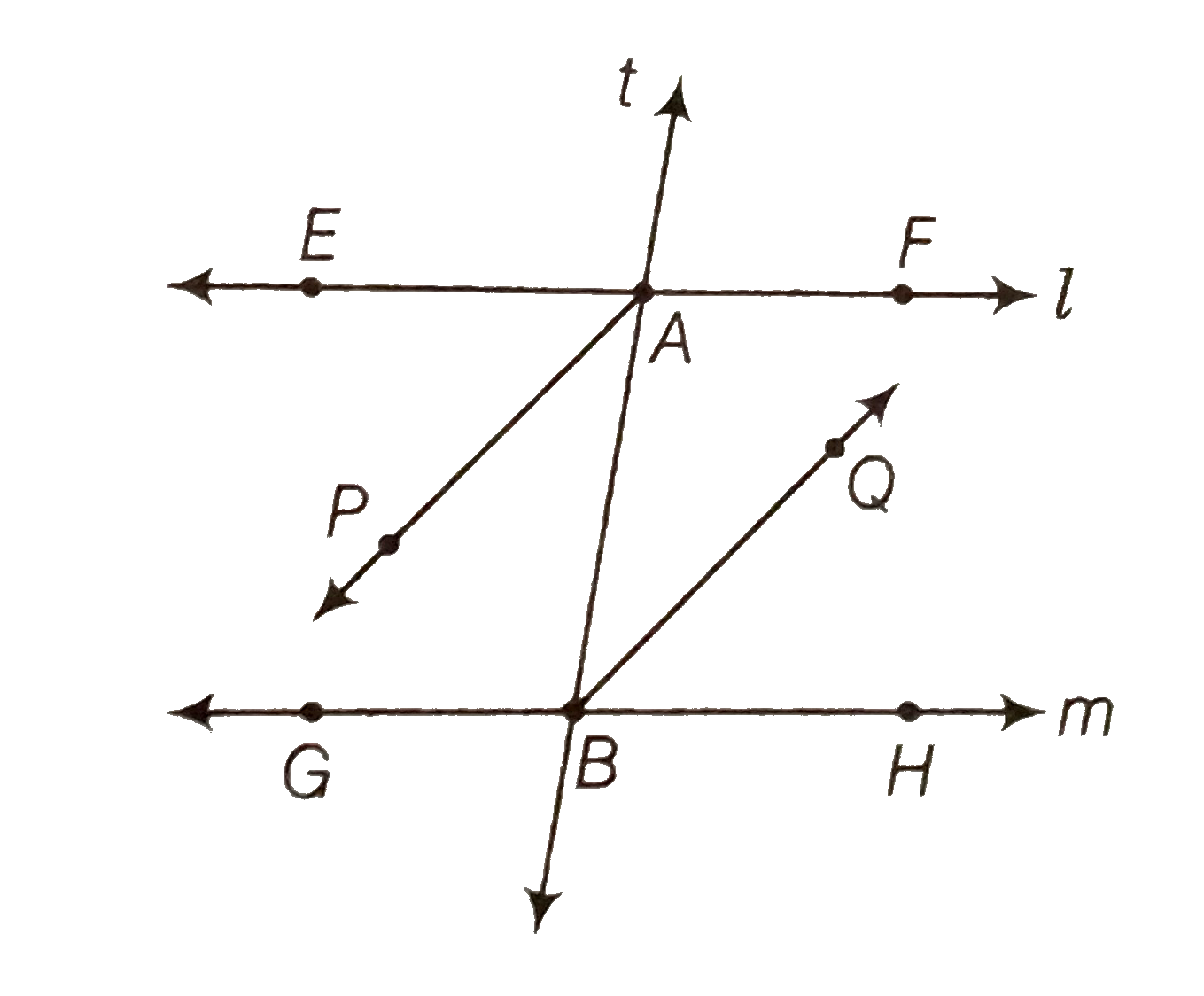
Related Playlists
Knowledge Check
- Question 1 - Select One
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 3:2, then the greater of the two angles is :
A72∘B36∘C108∘D44∘ - Question 1 - Select One
If a transversal line cuts two parallel lines then bisector of internal angle formed a
ArectangleBsquareCrhombusDparallelogram
Similar Questions
ABandCD are the disetors of the two alternate interior angle formed by the intersection of a trans versal 't' with parallel lines 'C' and 'm.' show that AB∣∣CD.
View SolutionWrite the converse of, "the alternate angles formed by two parallel lines and their transversal are congruent."
View SolutionState whether the statements are True or False.
Sum of interior angles on the same side of a transversal with two parallel lines is 90∘View SolutionIf the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
View SolutionState whether the statements are True or False.
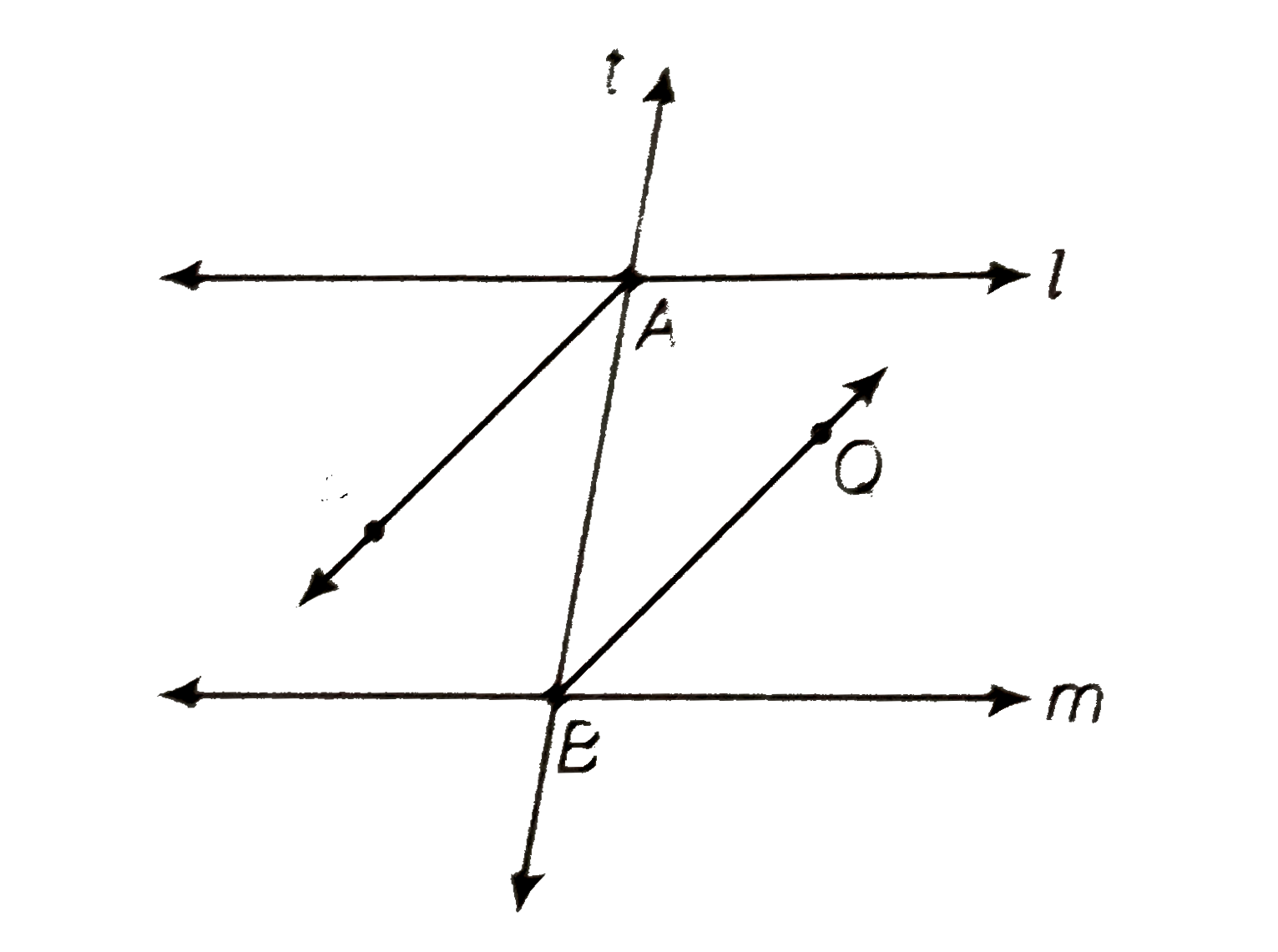
Interior angles on the same side of a transversal with two distinct parallel lines are complementary angles.View SolutionIn the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
 View Solution
View SolutionIf a transversal intersects two parallel lines, then
alternate interior angles are on the _______ side of the transversal.View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View Solution

