Consider an interference arrangement similar to YDSE. Slits S1 and S2 are illuminated with coherent microwave sources each of frequency 2 MHz. The sources are synchronised to have zero phase difference. The slits are separated by distance d= 75m. The intensity I(θ) is measured as a function of θ where θ is defined as shown in figure. if I0 is maximum intensity then calculated I(θ) for (i)θ=0∘,(ii)θ=π/6and(iii)θ=π/2
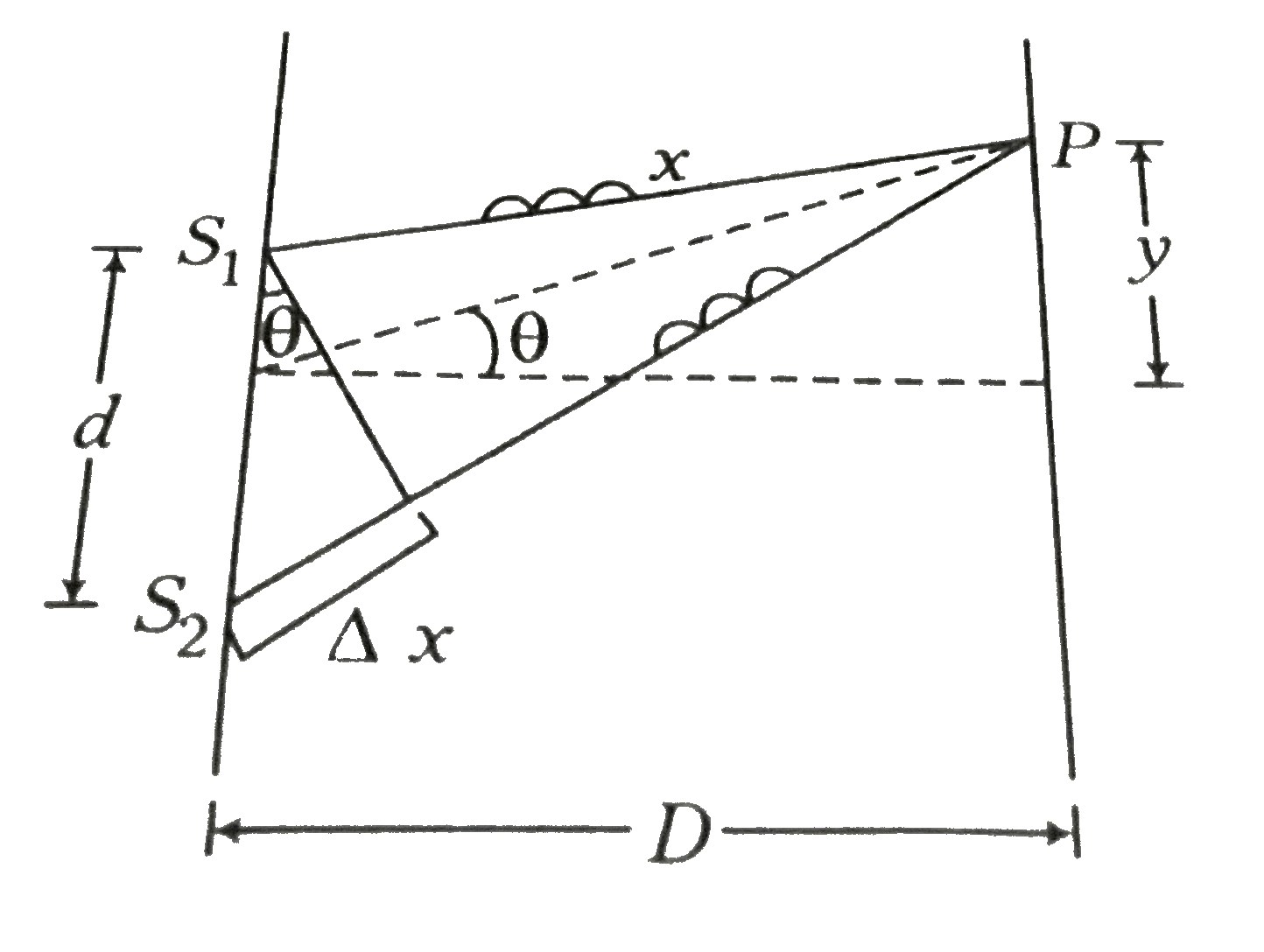
Given v=2 MHz=106 Hz d=75m
As, c=vλ
⇒λ=cv=3×1082×106=150m
Path difference Δx=dsinθ
Phase difference θ=2πλΔx=2πλdsinθ=2π150×75sinθ
=πsinθ
Intensity at point P, I=I0cos2(θ/2)=I0cos2(πsinθ2)
(i)θ=0,I=I0
(ii)θ=π6=30∘
I=I0cos2(πsin30∘2)=I0cos2(π/4)=I02
(iv)θ=π2=90∘,I=0
Related Playlists
Similar Practice Problems
- Question 1 - Select One
_E01_052_Q01.png)
In an interference arrangement similar to young's double slit experiment the slits S1 and S2 are illuminated with coherent microwave sources each of frequency 106Hz the sources are synchronized to have zero phase difference. the slits are separated by a distance d=150.0m. The intensity I(θ) is measured as a funtion of θ, where θ is defined as shown. if I0 is the maximum intensity then I(θ) for 0≤θ≤90∘ is given by:AI(θ)=I0/2 for θ=30∘BI(θ)=I0/4 for θ=90∘CI(θ)=I0 for θ=0∘DI(θ) is constant for all values of θ - Question 1 - Select One
In an interference arrangement similar to Young's double-slit experiment, the slits S_1 and S_2 are illuminated with coherent microwave sources, each of frequency 10^6 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0 m. The intensity I (theta) is measured as a function of theta, where theta is defined as shown. If I_0 is the maximum intensity, then I (theta) for 0lethetale90degree is given by
 AI(θ)=i02forθ=30degreeBi(θ)=I04forθ=90degreeCI(θ)=I0forθ=0degreeDI(θ) is constant for all
AI(θ)=i02forθ=30degreeBi(θ)=I04forθ=90degreeCI(θ)=I0forθ=0degreeDI(θ) is constant for all - Question 1 - Select One
In a interference arrangement similar to Young's double-slit experiment ,the slits S1 and S2 are illuminated with coheremt microwave source ,each of frequencies 106 Hz.The source are syhronized to have zero phase difference.The slits are separated by a distance from S1 and S2 where theta is defined as shown if I0 is the maximum intensity then
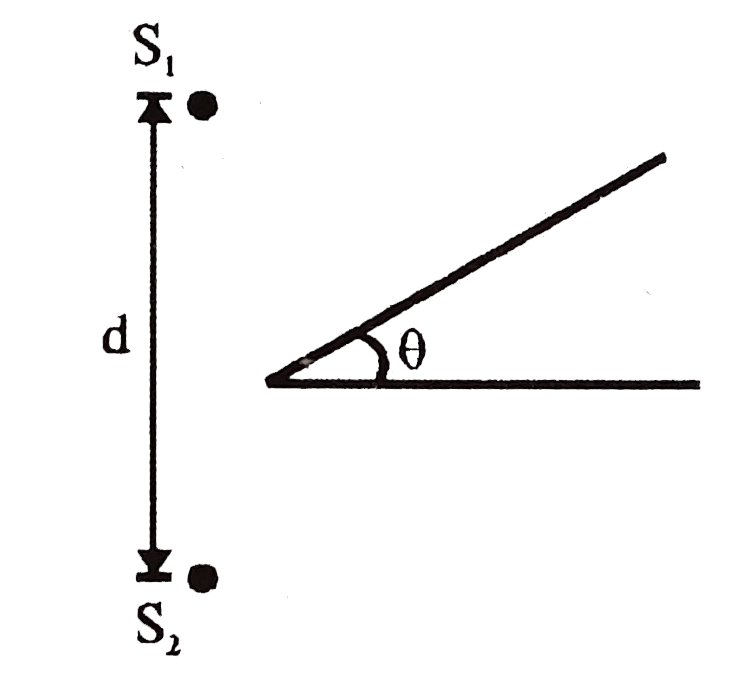 AI(θ)=I02 for θ=30∘BI(θ)=I04 for θ=90∘CI(θ)=(I0) for θ=90∘DI(θ) is constant for all value of θ
AI(θ)=I02 for θ=30∘BI(θ)=I04 for θ=90∘CI(θ)=(I0) for θ=90∘DI(θ) is constant for all value of θ - Question 1 - Select One
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P isAI0B9I0C3I0D8I0 - Question 1 - Select One
Consider interference between waves form two sources of intensities I&4I.Find intensities at point where the phase difference is π
AIB5IC4ID3I - Question 1 - Select One
The intensity of each coherent source is I0 . Which of the following gives the intensity at a point where the phase difference between the superposing waves is ϕ
AI0(1cosϕ)B2I0cos2(ϕ/2)C2I0(1+cosϕ)DI0cos2(ϕ/2)
Similar Questions
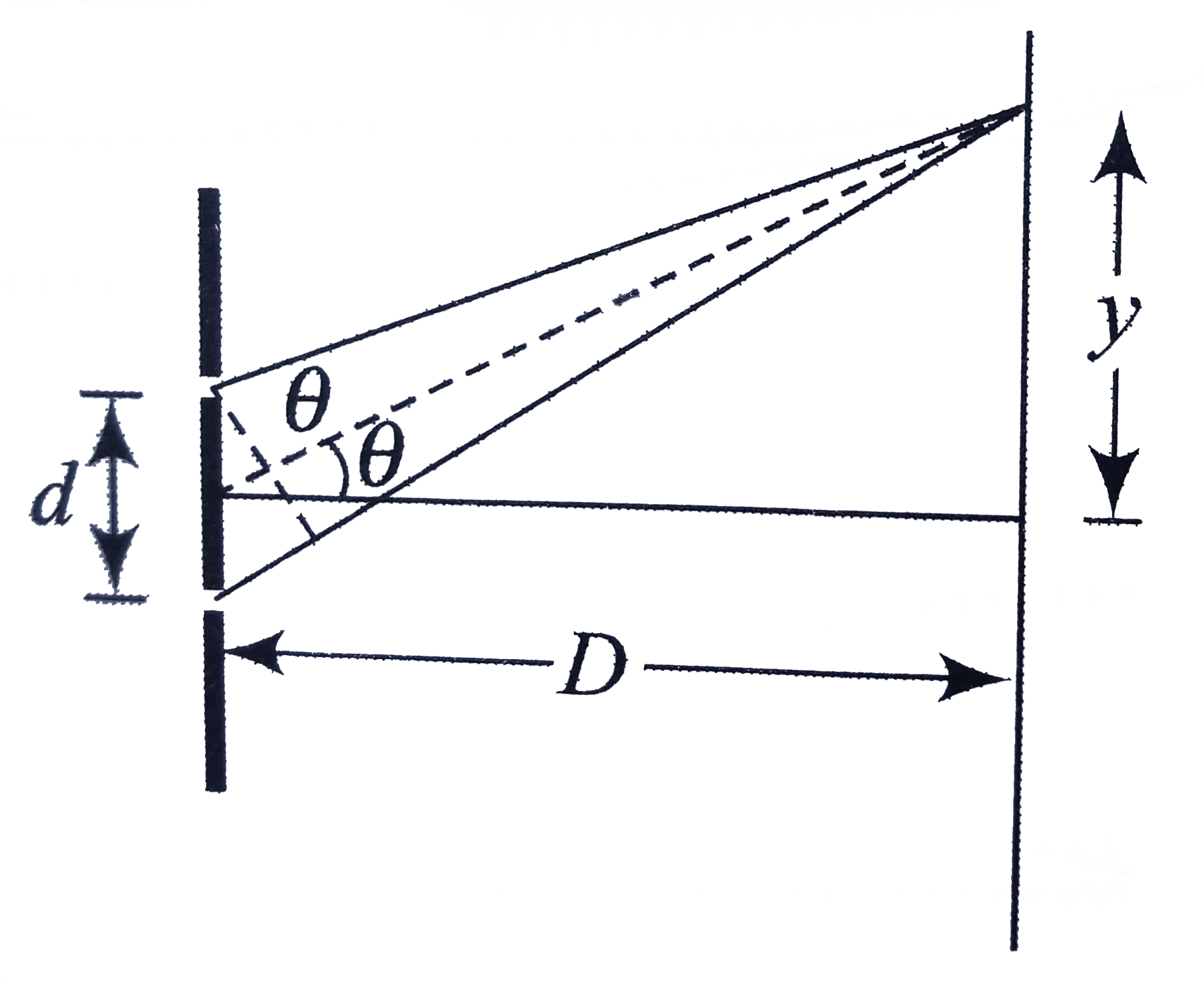
In an interference arrangement similar to double-slit experiment, S1 and S2 are illuminated with coherent source microwave source each of frequency 1 MHz. the sources are synchronized to have zero phase difference . This slits are separated by distance d=150.0m The intensity I(θ) is measured as a funciton of θ, where θ is defined as shown in figure. If I0 is maximum intensity, calculate I(θ)
For :
a. θ=0 b. θ=30∘
c. θ=90∘
 View Solution
View SolutionS1 and S2 are two coherent sources of frequency f each.(θ1=θ2=0∘)Vsound=330m/s.
(i) so that constructive interfence at 'p'
(ii) so that destructive interfrece at 'p'
 View Solution
View SolutionThe light from two coherent sources, each of intensity I, having a phase difference ϕ superimpose then resultant intensity (IR) of light is given as _____.
View SolutionIf θ=450, then :
(i) tan2θ+1sin2θ
(ii) cos2θ−sin2θView Solution

