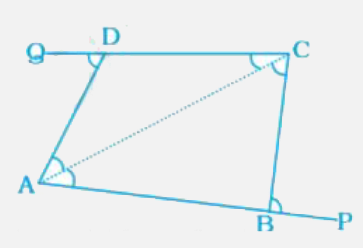
In Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
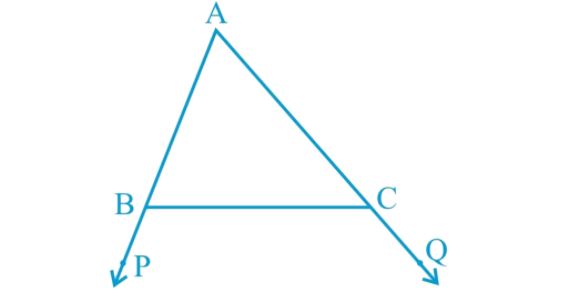
In the given figure,
∠ABC+∠PBC=180∘ [Linear pair of angles]
Also, ∠ABC=180∘−∠PBC ... (1)
∠ACB+∠QCB=180∘
[Linear pair]
∠ACB=180∘−∠QCB ... (2)
As ∠PBC<∠QCB (given),
180∘−∠PBC>180∘−∠QCB
∠ABC>∠ACB [From Equations (1) and (2)]
Thus, AC>AB (the Side opposite to the larger angle is larger).
Hence proved, AC>AB.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.18videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.54videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - Solved Examples9videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.810videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
The external bisector of ∠Band∠C of ΔABC(where AB and AC extended to E and F respectively) meet at point P. If ∠BAC=100∘, then the measure of ∠BPC is
A50∘B80∘C40∘D100∘
The sides AB and AC of a ABC are produced to P and Q respectively. If the bisectors of ∠PBC AND ∠QCB intersect at O, then ∠BOC=900−12∠A GIVEN : A ABC in which sides AB and AC are produced to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at O.
View SolutionConsider a triangle ABC. The sides AB and AC are extended to points D and E respectively, such that AD=3ABandAE=3AC. Then one diagonal of BDEC divides the other diagonal in the ratio p:q then p+q=
View SolutionIn ABC and PQR Figure, AB=PQ,BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX =∠PQY. Prove that ABC≅PQR. Figure
View SolutionThe sides AB and AC of ABC are product to P and Q respectively. the bisectors of exterior angles at B and C of ABC meet at O (fig.19) prove that ∠BOC=900−12∠A
View SolutionIn Fig. 10.20, the sides AB, BC and CA of triangle ABC touch a circle with centre O and radius r at P, Q and R respectively. (FIGURE) Prove that: 1) AB + CQ = AC + BQ 2) Area (ABC) = (r/2)*(Perimeter of ABC)
View SolutionIn Fig.100, ABCD and EF is a transversal intersecting AB and CD at P and Q respectively. The measure of ∠DOP is (a) 65 (b) 25 (c) 115 (d) 105
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
 View Solution
View Solution