ABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
Given ΔABC is a right angled triangle with AB= AC ,AD is the bisector of ∠A
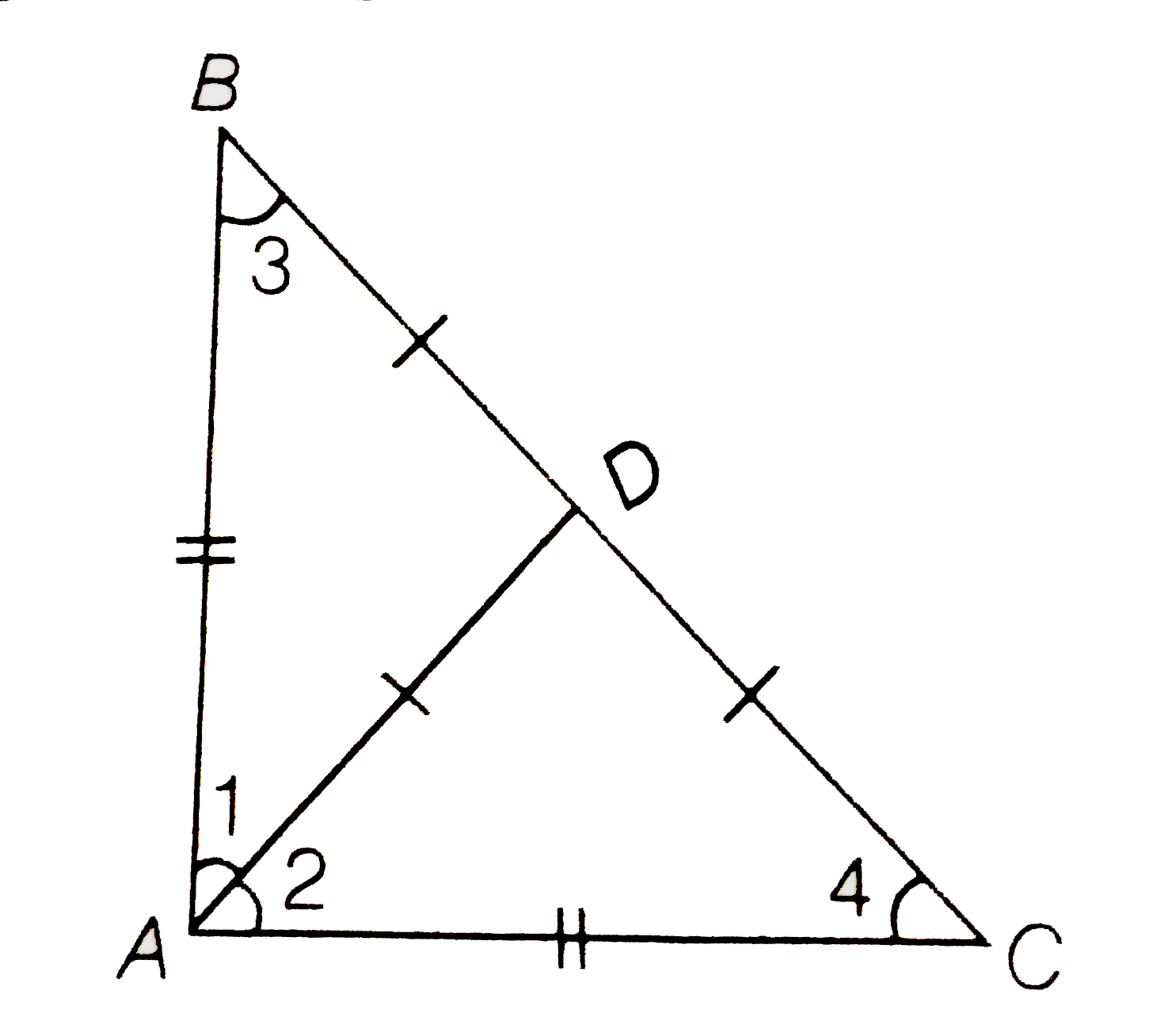
To Prove BC =2 AD
Proof in ΔABC AB=AC [given ]
⇒ ∠C=∠B....(i)
[angle opposite to equal sides are equal ]
NOW ,in right angled ΔABC,∠A+∠B+∠C=180∘
[by angle sum property of a triangle in 180∘]
⇒90∘+∠B+∠B=180∘ [from Eq (i)]
⇒2∠B=90∘
⇒∠B=45∘
⇒∠B=∠C=45∘
or ∠3=∠4=45∘ [∵ AD is bisector of∠A]
∵∠1=∠2=45∘
Now ∠1=∠3,∠2=an≥l4
⇒BD=AD,DC=AD
[side opposite to equal angles are eaqual ]
Hence,BC=BD+CD = AD + AD⇒ BC=2 AD [from Eq.(ii)]
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS11videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS8videos
VOLUME AND SURFACE AREA
Similar Questions
Knowledge Check
- Question 1 - Select One
In right triangle, ABC, AB=10,BC=8,AC=6.
A35B34C45D54
ΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionTriangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : ABPQ=ADPM
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionGiven a triangle ABC with AB=2 and AC=1. Internal bisector of ∠BAC intersects BC at D. If AD = BD and Δ is the area of triangle ABC, then find the value of 12Δ2.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View Solution
