An atrangement of source charges produces electric. potential along the x -axis, where V is in volt and is in metre. If a charge particle of mass 1g1nC is present in this field and its turning points are at , then what is the particie's maximum speed (in mm/s).
The correct Answer is:8
Related Playlists
Knowledge Check
- Question 1 - Select One
A charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
A B
B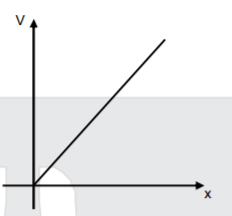 C
C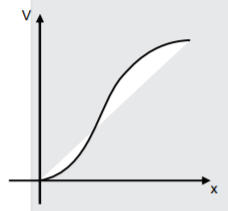 D
D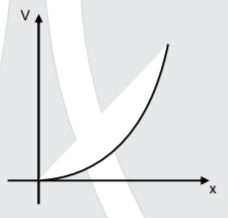
- Question 1 - Select One
There exist uniform magnetic and electric fields of magnitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
A(0,1,2)mB(0,−π2/2,−2)mC(2,π2/2,2)mD(0,π2/2,2)m - Question 1 - Select One
A point charge q produces an electric field of magnitude 2NC−1 at a point distance 0.25 m from it. What is the value of charge ?
A1.39×10−11CB1.39×1011CC13.9×10−11CD139×1011C - Question 1 - Select One
In a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point 2a, b/2, 0 its speed becomes 2v. Find the value of electric field strength of m, v and co-ordinates.
A32mv2qaBmv2qaC2mv2qBaD32vB - Question 1 - Select One
A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
A|E|=|B| and the two field are perpendicularB|E|=v|B| and the two field are perpendicularC|B|=v|E| and the two field are parallelD|B|=v|E| and the two fields are perpendicular
Similar Questions
A charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point( 2a, b/2, 0) its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
View Solution

