ABC is a equilateral triangle and CD is internal bisector of ∠C. If DC is extended to E in such a way that AC = CE then ∠CAE is-
A
75∘
B
30∘
C
15∘
D
45∘
Video Solution
|
Answer
Step by step video & image solution for ABC is a equilateral triangle and CD is internal bisector of angleC. If DC is extended to E in such a way that AC = CE then angleCAE is- by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023
Related Playlists
Similar Practice Problems
- Question 1 - Select One
ABC is a equilateral triangle and CD is internal bisector of ∠C. If DC is extended to E in such a way that AC = CE then ∠CAE is-
A45∘B75∘C30∘D15∘ - Question 1 - Select One
ABC is a equilateral triangle and CD is internal bisector of ∠C. If DC is extended to E in such a way that AC = CE then ∠CAE is-
A45∘B75∘C30∘D15∘ - Question 1 - Select One
CF is the internal bisector of angle C of ΔABC then CF is equal to
A2aba+bcosC2Ba+b2abcosC2CbsinAsin(B+C2)Dnone of these - Question 1 - Select One
In a triangle ABC, D is a point on BC such that AD is the internal bisector of ∠A. Let ∠B=2∠C and CD = AB. Then ∠A is
A18∘B36∘C54∘D72∘ - Question 1 - Select One
In △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
A3:5B4:5C1:2D2:1 - Question 1 - Select One
In a triangle ABC, internal bisector of ∠ABC and external bisector of ∠ACB meet in D. Which one of the following is true ?
A∠BDC=∠BACB∠BDC=12∠ABCC∠BDC=∠DBCDNone of these
Similar Questions
If in a triangle ABC,CD is the angular bisector of the angle ACB then CD is equal to
View SolutionIn a ΔABC it is given AD is internal bisector of ∠A . If BD=4cm,DC=5cmandAB=6cm, then AC =?
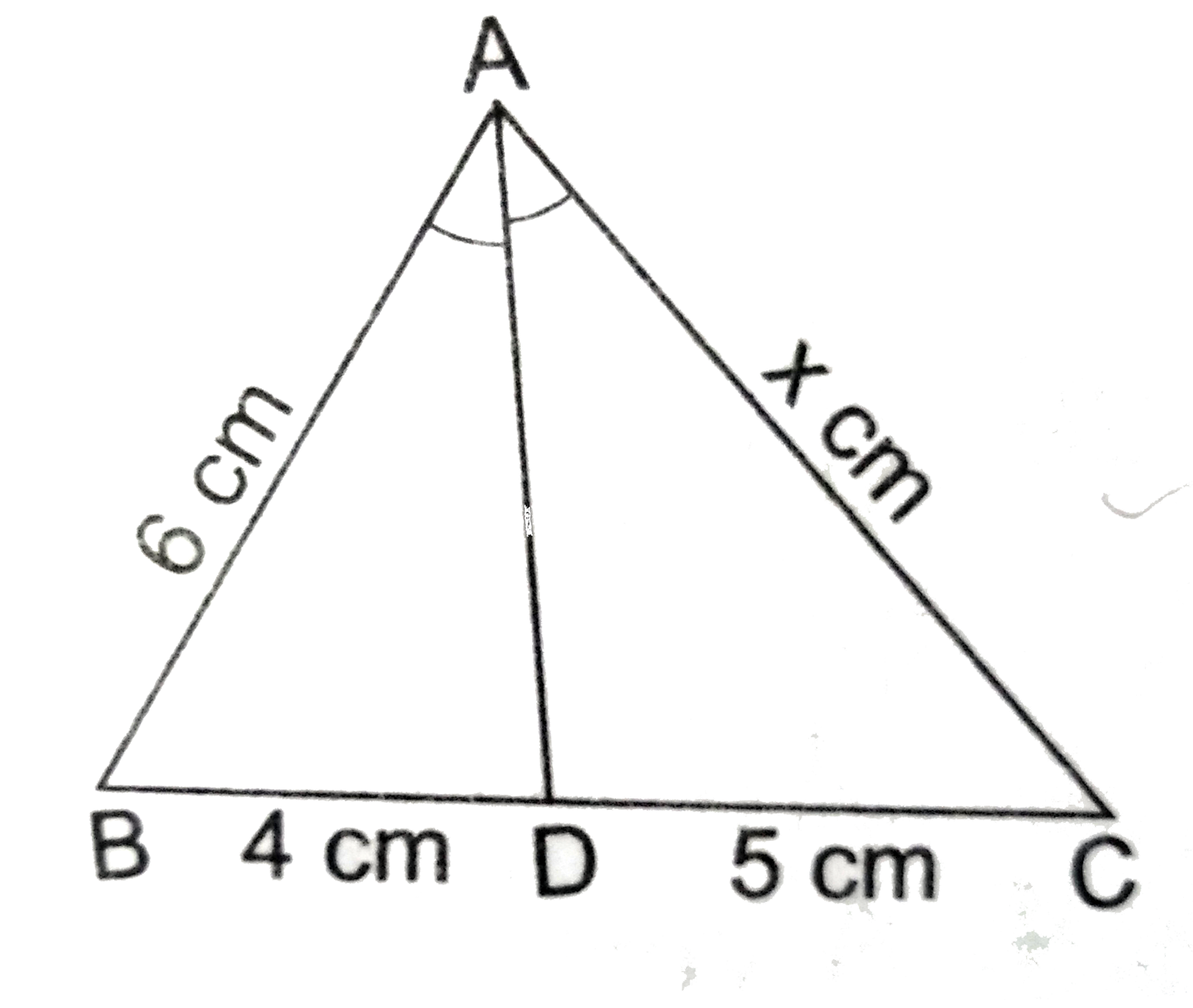 View Solution
View SolutionIn a ΔABC, it is give ttha AD is the internal bisector of ∠A. If AB=10cm,AC=14cmandBC=6cm then CD=?
 View Solution
View SolutionProve that the internal bisector of the angle A of a triangle ABC divides BC in the ratio AB:AC
View Solution

