Force Between The Plates Of A Parallel Plate Capacitor
Step by step video & image solution for Force Between The Plates Of A Parallel Plate Capacitor by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Practice Problems
- Question 1 - Select One
As the distance between the plates of a parallel plate capacitor decreased
Achances of electrical break down will increases if potential difference between the plates is kept constant.Bchance of electrical break down will decreases if potential difference between the plates is kept constant.Cchance of electric break down will increases if charge on the plates is kept constantDchance of electrical break down will decrease if charge on the plate is kept constant. - Question 1 - Select One
The expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)
 Aε0A(d1K1+d2K2+d3K3)Bε0A(d1+d2+d3K1+K2+K3)Cε0A(K1K2K3)d1d2d3Dε0(AK1d1+AK2d2+AK3d3)
Aε0A(d1K1+d2K2+d3K3)Bε0A(d1+d2+d3K1+K2+K3)Cε0A(K1K2K3)d1d2d3Dε0(AK1d1+AK2d2+AK3d3) - Question 1 - Select One
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases - Question 1 - Select One
The expression for the capacity of a capacitor formed by placing a compound dieletric between the plates of a parallel plate capacitor, as shown in figure , will be (Given area of plate = A)
 Aε0A(d1K1+d2K2+d3K3)Bε0A(d1K1+d2K2+d3K3)Cε0A(K1K2K3)(d1d2d3)Dε0(AK1d1+AK2d2+AK3d3)
Aε0A(d1K1+d2K2+d3K3)Bε0A(d1K1+d2K2+d3K3)Cε0A(K1K2K3)(d1d2d3)Dε0(AK1d1+AK2d2+AK3d3) - Question 1 - Select One
Force of attraction between the plates of a parallel plate capacitor is
Aq22ε0AKBq2ε0AKCq2ε0ADq22ε0A2K - Question 1 - Select One
In the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
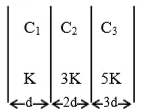 A1534Kε0AdB156Kε0AdC256Kε0A6D96Kε0Ad
A1534Kε0AdB156Kε0AdC256Kε0A6D96Kε0Ad
Similar Questions
The distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure will be
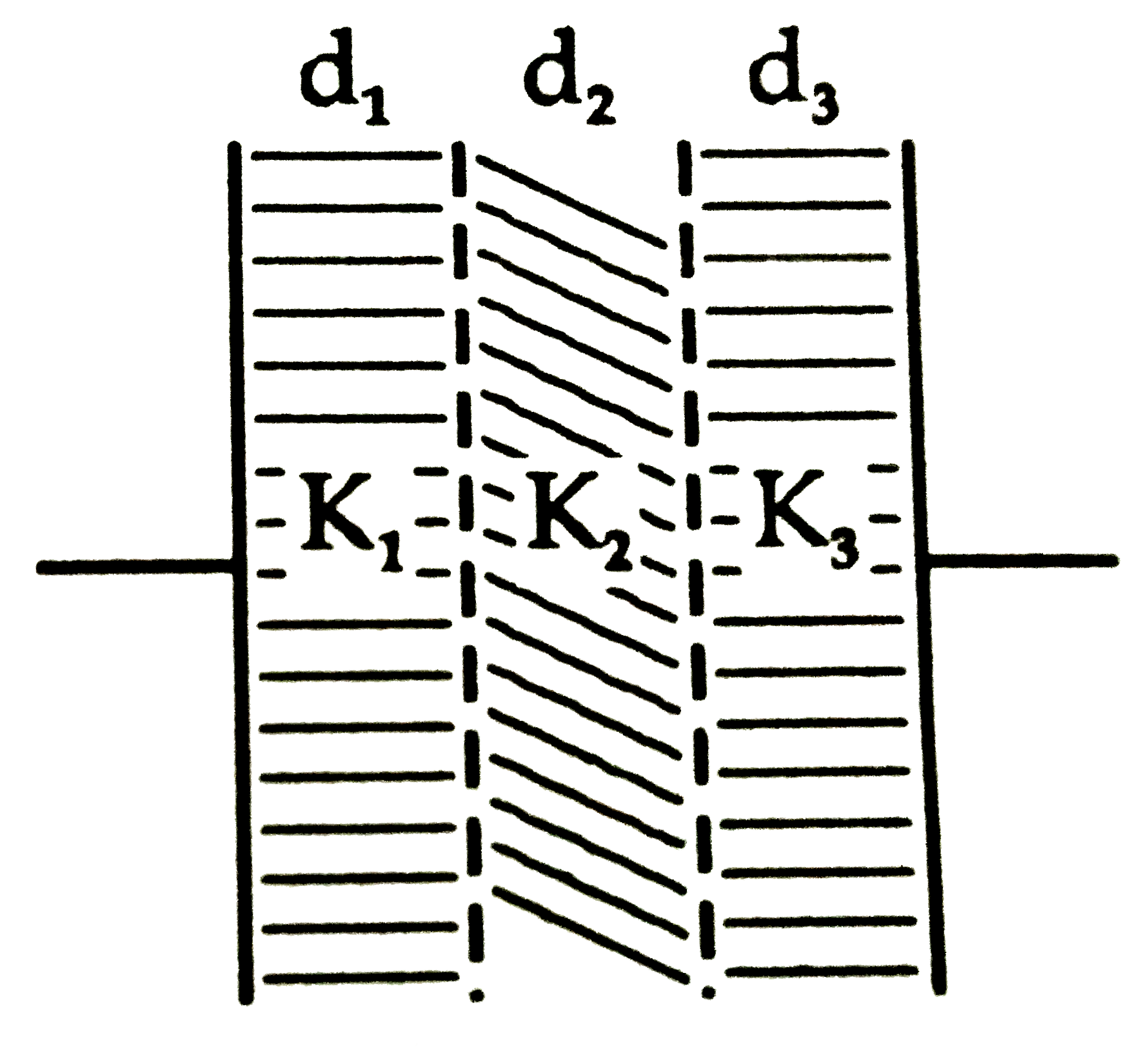 View Solution
View Solution

