For any three non-zero vectors →a,→b and →c if ∣∣(→a×→b).→c∣∣=|→a|∣∣→b∣∣|→c| then →a.→b+→b.→c+→c.→a=
→a.→b=→b.→c=→c.→a≠0
→a.→b=0 only
→b.→c=0 only
→a.→b=→b.→c=→c.→a=0
The correct Answer is:D
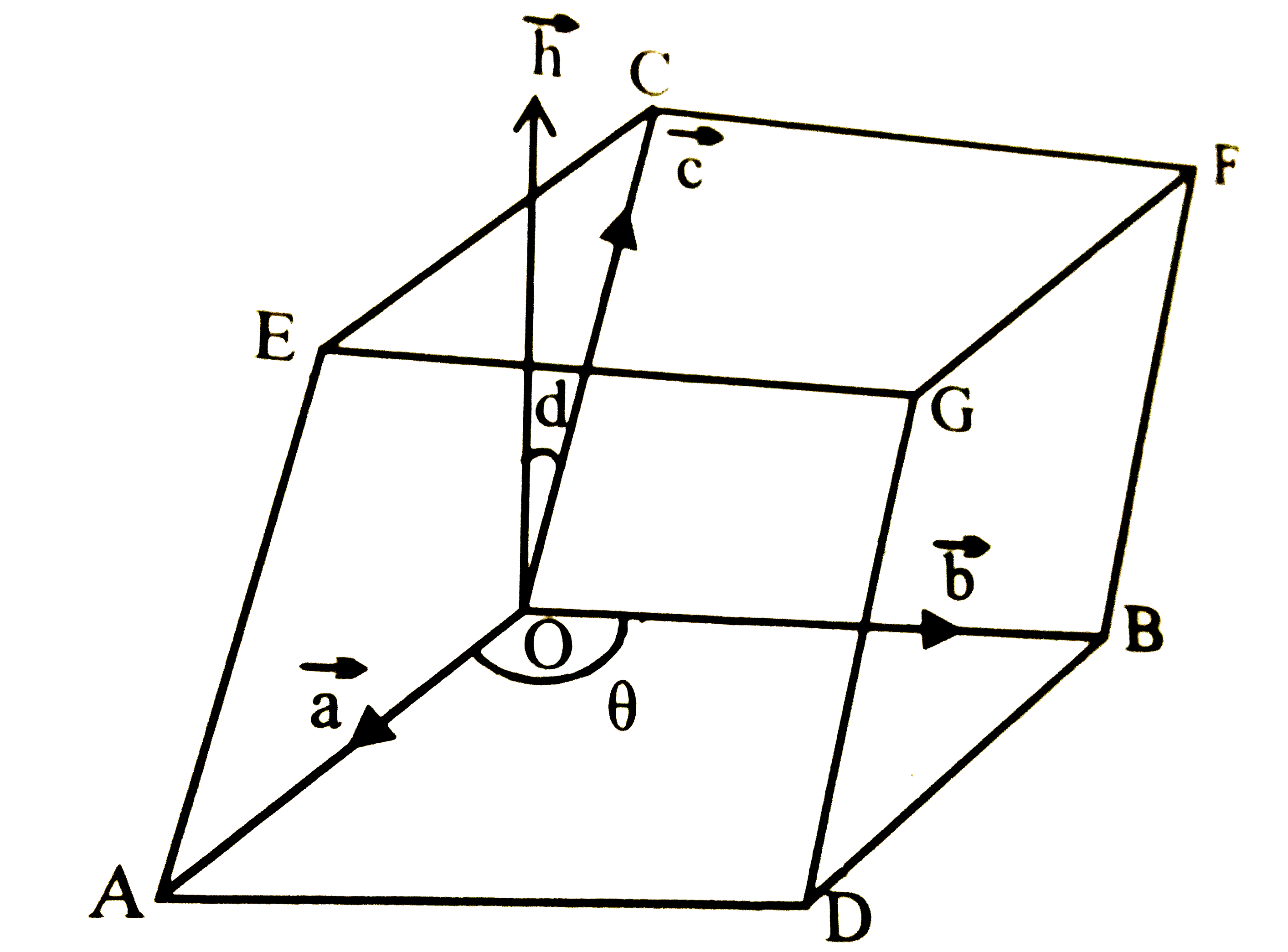
Refer to the figure.
∣∣(→a×→b).→c∣∣ is triple dot product and is volume (V) of the parallelepiped whose adjacent edges are a, b, and c.
i.e., V=∣∣(→a×→b)∣∣.→OC
⇒V=|→a|∣∣→b∣∣(sinθ)(cosϕ)|→c|
where 0≤θ≤π is the angle between →aand→b.
As given
∣∣(→a→b).→c∣∣=|→a|∣∣→b∣∣|→c|
⇒|sinθcosϕ|.=1
⇒sinθ=1,cosϕ=1
⇒θ=π2,ϕ=0
⇒→a.→b.=0=→b.→c=→c.→a
Related Playlists
Knowledge Check
- Question 1 - Select One
For non zero vectors →a,→b,→c
∣∣∣(→a×→b).−−−→|=|→a∣∣∣∣∣→b∣∣|→c| holds iffA→a.→b=→b.→c=→a.→a=0B→a.→b=0=→b.→cC→b.→c=0=→c.→aD→c.→a=0=→a.→b - Question 1 - Select One
If →a,→b,→c are three vectors such that
→a+→b+→c=→0,|→a|=1∣∣→b∣∣=2,|→c|=3 , then
→a.→b+→b.→c+→c+→c.→a is equal toA1B0C-7D7 - Question 1 - Select One
If →a+2→b+3→c=→0 then →a×→b+→b×→c+→c×→a=
A2(→a×→b)B6(→b×→c)C3(→c×→a)D→0 - Question 1 - Select One
Statement 1: If V is the volume of a parallelopiped having three coterminous edges as →a,→b, and →c, then the volume of the parallelopiped having three coterminous edges as
→α=(→a.→a)→a+(→a.→b)→b+(→a.→c)→c
→β=(→a.→b)→a+(→b.→b)→b+(→b.→c)→c
→γ=(→a.→c)→a+(→b.→c)→b+(→c.→c)→c is V3
Statement 2: For any three vectors →a,→b,→c
∣∣ ∣ ∣∣→a.→a→a.→b→a.→c→b.→a→b.→b→b.→c→c.→a→c.→b→c.→c∣∣ ∣ ∣∣=[→a→b→c]3A1B2C3D4 - Question 1 - Select One
If →a,→b,→c are the 3 vectors such that |→a|=3,∣∣→b∣∣=4,|→c|=5,∣∣→a+→b+→c∣∣=0 then the value of →a.→b+→b.→c+→c.→a is :
A-20B-25C25D50
Similar Questions
For non zero vectors →a,→b,→c∣∣(→a×→b).→c∣∣=|→a|∣∣→b∣∣∣→∣∣ holds if and only if (A) →a.→b=0,→b.→c=0 (B) →b.→c=0,→c.→a=0 (C) →c.→a=0,→a.→b=0 (D) →a.→b=→b.→c=→c.→a=0
View SolutionIf →a,→b,→c are three vectors such that →a+→b+→c=0and|→a|=5,∣∣→b∣∣=12.|→c|=13, then find →a→b+→b→c+→c→a
View SolutionIf →a,→band→c be any three non coplanar vectors. Then the system of vectors veca\',vecb\' and vecc\'whichsatiiesveca.veca\'=vecb.vecb\'=vecc.vecc\'=1 →a.→b'=→a.→a'=→b.→a'=→b.→c'=→c.→a'=→c.→b'=0 is called the reciprocal system to the vectors →a,→b,and→c. The value of (→a×→a')+(→b×→b)+(−→×→') is (A) →a+→b+→ (B) →a'+→b'+→' (C) 0 (D) none of these
View SolutionFor any two vectors →a and →b prove that ∣∣→a×→b∣∣2=∣∣∣→a.→a→a.→b→b.→a→b.→b∣∣∣
View SolutionIf →a,→band→c be any three non coplanar vectors. Then the system of vectors veca\',vecb\' and →c' which satisfies →a.→a'=→b.→b'=→c.→c'=1→a.→b'=→a.→a'=→b.→a'=→b.→c'=→c.→a'=→c.→b'=0 is called the reciprocal system to the vectors →a,→b,and→c. The value of [→a'→b'→c']−1 is (A) 2[→a→b→c] (B) [→a,→b,→c] (C) 3[→a→b→c] (D) 0
View Solution

